Tangenta la graficul ecuației funcțiunilor tangente
Luați în considerare următoarea imagine:
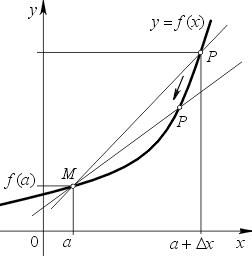
Aceasta reprezintă o funcție y = f (x), este diferențiabilă în punctul a. Marcat de punctul M cu coordonatele (a; f (a)). Printr-un punct P arbitrar (a + Ax; f (a + Ax)) generat transportate MR secant.
Dacă acum punctul P pe programul de deplasare la punctul M, atunci linia LL va oscila în jurul acestui punct M. Când bH va tinde la zero. Din aceasta putem formula definiția tangenta la graficul functiei.
Tangenta la graficul funcției
Tangenta la graficul funcției are o poziție limită a secțiunii transversale tinde la zero creștere a argumentului. Trebuie înțeles că existența derivatei f la x0 înseamnă că, la acest punct graficul are o tangentă la ea.
Coeficientul unghiular al tangentei este egală cu derivata funcției în punctul f „(x0). Acesta este sensul geometric al derivatului. Tangenta la graficul de la punctul x0 funcțiile derivabile f - este o linie care trece prin punctul (x0; f (x0)) și având un coeficient unghiular f „(x0).
Ecuația tangentei
Să încercăm să obținem ecuația de tangenta la graficul unei funcții f la punctul A (X0; f (x0)). Ecuația unei linii cu panta k este după cum urmează:
Din moment ce avem o pantă egală cu derivatul f „(x0). ecuația ia forma: y = f „(x0) * x + b.
Acum vom calcula valoarea b. Pentru aceasta folosim faptul că funcția trece prin punctul A.
f (x0) = f '(x0) * x0 + b, b și deci exprimă obține b = f (x0) - f' (x0) * x0.
Substitut valoarea obținută în ecuația tangentei:
y = f '(x0) * x + b = f' (x0) * x + f (x0) - f '(x0) * x0 = f (x0) + f' (x0) * (x - x0).
y = f (x0) + f „(x0) * (x - x0).
Luați în considerare următorul exemplu: găsi ecuația tangentei la graficul funcției f (x) = x 3 - 2 * x 2 + 1 x = 2.
2. f (x0) = f (2) = 2 2 - 2 * 2 2 + 1 = 1.
3. f „(x) = 3 * x 2 - 4 * x.
4. f '(x0) = f' (2) = 3 * 2 2 - 4 * 2 = 4.
5. Substituind valorile obținute în formula tangentei, obținem: y = 1 + 4 * (x - 2). Extinderea parantezele și citând termeni similari obținem: y = 4 * x - 7.
Schema generală de preparare a ecuației tangentei la graficul y = f (x):
1. Determinarea x0.
2. Se calculează f (x0).
3. Se calculează f „(x)
4. Se calculează f „(x0)
5. Înlocuind valorile în ecuația tangentei y = f (x0) + f „(x0) * (x - x0).