site-ul personal - o tangentă la graficul
Tangenta la graficul funcției
Tangent - o linie care trece prin punctul curbei și coincide cu ea în acest moment până la primul ordin (figura 1).
O altă definiție. această poziție de limitare a secantă când → 0 Ax.
Explicație. Să considerăm linia dreaptă intersectează curba la două puncte A și B (a se vedea figura). Această transversală. Să-l rotiți în sens orar până când până când se va găsi doar un singur punct comun cu curba. Deci, avem o tangentă.
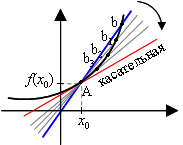
definiție strictă a unei tangente:
Partia are o forma y = kx directă + b. Coeficientul k este o pantă a liniei.
Panta este egală cu tangenta unghiului ascuțit format de linia dreaptă cu abscisa:
Aici, unghiul α - este unghiul dintre linia y = kx + b și un rezultat pozitiv (adică invers acelor de ceasornic), direcția de abscisă. El a numit unghiul de înclinare al liniei (Figura 1 și 2).
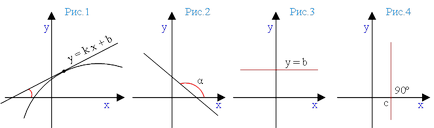
Dacă unghiul de înclinare al liniei y = kx + b obtuz, coeficientul unghiului este un număr negativ. Scăderi grafic (Figura 2).
Dacă o linie paralelă cu axa X, unghiul de înclinare al liniei este zero. În acest caz, panta liniei este de asemenea egal cu zero (deoarece tangenta la zero este zero). Ecuația liniei are forma y = b (Fig.3).
Dacă unghiul liniei este 90º (π / 2), adică este perpendiculară pe axa x, linia definită de ecuația x = c. unde c - un număr real (Figura 4).