Ntsialnaya și componenta normală a accelerației

Componentele tangențiale și normale de accelerare

Accelerare - mărime vectorială ce caracterizează viteza unui corp în mișcare schimbă viteza în mărime și direcție.

Medie de puncte de accelerare în intervalul de timp este AT ASR vectorul. este egal cu raportul Av sporului vectorului de viteză la interval AT.

Accelerația (accelerația instantanee) a punctului se numește o mărime vectorială a. egală cu un prim derivat al vitezei v în raport cu timpul (sau al doilea derivat al razei - vector în timp).

accelerare la momentul t egală cu accelerația medie punct limită în cursul

Într-un sistem de coordonate cartezian, vectorul poate fi scris în ceea ce privește coordonatele sale:

Unitate vector accelerație

Vectorul poate fi reprezentat ca suma a două componente:

- componenta tangențială a accelerației este direcționată de-a lungul tangenta la traiectoria punctului și este egală cu

unde vectorul - tangenta vectorul unitate tras într-un punct al traiectoriei și direcția vitezei

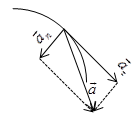
Vectori și codirectional cu mișcare uniform accelerată; la acel atunci când mișcarea ravnozamedlennom.

accelerația tangențială - caracterizează viteza de schimbare a modulului vectorului de viteză al punctului (caracterizează viteza de modificare a dimensiunii).

Pentru mișcare uniformă.

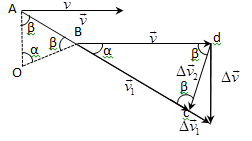
-componentă normală a accelerației (accelerația) este direcționată de-a lungul normalei la traiectoria și punctul considerat în direcția centrului de curbură a traiectoriei. O traiectorie curbă poate fi reprezentat ca un set de porțiuni elementare, dintre care fiecare poate fi considerată ca un arc de circumferință cu raza R (raza de curbură numită punct dat al curbei traiectoriei în circumferință)

accelerație normală caracterizează rata de schimbare a direcției vectorului de viteză (indică modificarea vitezei direcției).

Modul accelerație maximă:

Clasificarea depinde de mișcările componentelor tangențiale și normale:

§5 Cinematica mișcării de rotație

Rotirea corpului la un unghi φ poate fi descris printr-un vector a cărui lungime este egală cu cp. și direcția coincide cu axa de rotație și definită de regula din dreapta șurub (degetul mare, mana dreapta):

Patru degete de la mâna dreaptă - direcția de rotație, degetul mare îndoit indică direcția vectorului.

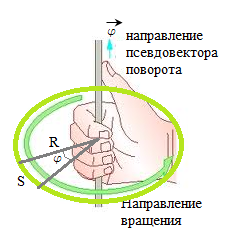
Direcția de rotație a vectorului cp, este asociat cu direcția de rotație a regulii mâinii drepte. Astfel de vectori sunt denumiți axial (axial) sau pseudovectors pentru a le distinge de (numite uneori câmp) vectori normali. Este viteza unghiulară vector care este numeric egal cu primul derivat al unghiului de rotație în raport cu timpul t și este direcționat de-a lungul unei axe fixe pe regula dreapta.

Viteza unghiulară. precum și un vector axial. Vectorii axiale au anumite puncte de aplicare, acestea pot fi depuse din orice punct al axei de rotație. Adesea, acestea stabilesc un punct fix al axei de rotație, la începutul raportului primit de sistem de coordonate simultan. rotirea corpului se numește uniform dacă.

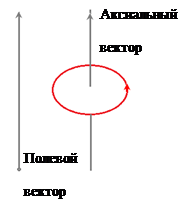
Puncte de viteză în contrast cu viteza unghiulară. corp numita viteză liniară. Acesta este direcționat perpendicular atât pe axa de rotație (adică un vector) și raza - R. vectorul Conectabil la punctul P din centrul cercului O și egal cu produsul vectorial al:

rotație uniformă poate caracteriza perioada de rotație T, prin care să înțeleagă momentul în care corpul face o revoluție, și anume, se rotește. Apoi - conectarea a vitezei unghiulare cu perioada de circulație.

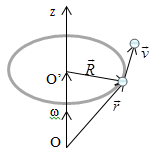
frecvența de rotație - numărul de rotații pe unitatea de timp; .

În cazul mișcării de rotație alternativ a vitezei unghiulare a punctului material nu se schimbă, atât în ​​mărime și direcție. Pentru a caracteriza viteza de schimbare a vitezei unghiulare de rotație neuniformă în jurul unei axe fixe este inserat vectorul accelerație unghiulară a unui corp egal cu primul derivat al vitezei sale unghiulare în timp.

Vectorul de asemenea, este un axial (sau pseudovector). Vectori și codirectional cu rotație accelerată () și oppositely îndreptate cu rotație lentă.

()

Accelerarea unui punct P arbitrar al corpului, în contrast cu accelerația unghiulară a corpului se numește o accelerație liniară.

Pentru mișcarea de rotație uniform accelerată se poate scrie:

Relația dintre măsurătorile liniare și unghiulare: