Ecuația tangentei la graficul funcției

§ 34. Ecuația tangentei la graficul

În § 32 menționat că, dacă punctul M (a, f (a)) aparține graficului funcției y = f (x), iar în cazul în care, în acest moment la graficul funcției se poate trage o tangentă nu este perpendiculară pe axa x, panta tangentei este egal cu f „(a). Am folosit acest lucru de câteva ori. De exemplu, în § 33, sa constatat că graficul funcției y = sin x (undă sinusoidală) la origine face cu unghiul axa x 45 ° (mai precis, o tangentă la graficul la origine este direcția pozitivă a unghiului axei x 45 °) și exemplul 5 § 33 puncte au fost găsite pe funcția graficului dat. unde tangenta este paralelă cu abscisa. În Exemplul 2, § 33 a fost compus ecuația tangentei la graficul funcției y = x 2 x = 1 (mai precis, la punctul (1, 1), dar de multe ori indică doar valoarea abscisei, presupunând că în cazul în care valoarea abscisei este cunoscută, atunci valoarea ordonata pot fi găsite din ecuația y = f (x)). În această secțiune vom dezvolta un algoritm de elaborare a ecuației programul kasatelnoy.k orice funcție.

Să presupunem că funcția y = f (x) și un punct M (a, f (a)), și este de asemenea cunoscut faptul că există f „(a). Noi construim ecuația de tangenta la funcția graficului dat într-un anumit punct. Această ecuație, așa cum Equation orice linie care nu este paralela cu axa ordonata este y = kx + m, deci provocarea este de a găsi valorile coeficienților k și m.

Pe panta există o problemă: știm că o = f „(a). Pentru a calcula valorile m folosim faptul că linia dorită trece prin punctul M (a, f (a)). Aceasta înseamnă că, dacă înlocuim coordonatele punctului M în ecuația liniei, obținem ecuația corectă: f (a) = ka + m, unde descoperim că m = f (a) - ka.
Rămâne să înlocuiască valorile coeficienților de balene găsit într-o ecuație liniară:

Am obținut o ecuație a tangentei la graficul funcției y = f (x) la x = a.
Dacă, să zicem,
Substituind în ecuația (1), valorile obținute a = 1, f (a) = 1, f „(a) = 2, obținem: y = 1 + 2 (x-f), adică, y = 2x-1.
Comparați acest rezultat cu ceea ce s-a obținut în exemplul 2 din § 33. Desigur, ea a ieșit la fel.
Construirea ecuatia tangentei la graficul funcției y = tg x la origine. Avem așadar cos x f '(0) = 1 Substituind în ecuația (1), valorile obținute a = 0, f (a) = 0, f' (a) = 1, obținem: y = x.
De aceea, ne-am petrecut tangensoidu în § 15 (vezi. Fig. 62), prin origine, la un unghi de 45 ° față de axa orizontală.
Rezolvarea acestor exemple destul de simplu, am folosit de fapt un algoritm specific, care este încorporată în formula (1). Să facem acest algoritm clar.

ALGORITMUL DE tangent ECUAȚIE la graficul funcției y = f (x)

1) reprezintă abscisa punctului de tangență cu litera a.
2) Se calculează 1 (a).
3) Găsiți f '(x) și se calculează f' (a).
4) Se umple cu rezultatele a, f (a), (a) în formula (1).

Exemplul 1. Crearea ecuație a tangentei la graficul funcției x = 1.
Decizie. Noi folosim algoritmul, dat fiind faptul că în acest exemplu,

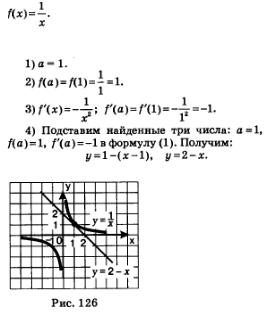
Fig. 126 prezintă o hiperbolă. construit y liniar = 2.
Calculele de desen prezentat confirmă: într-adevăr, linia y = 2 Referitor la hiperbola la punctul (1, 1).

A: y = x 2.
Exemplul 2 La un grafic al unei tangente, astfel încât să fie paralelă cu linia y = 4 - 5.
Decizie. formularea mai precisă a problemei. Cerința pentru „a tangentă“ înseamnă de obicei „pentru a face ecuația tangenta.“ Acest lucru este logic, pentru că dacă o persoană este capabil să lucreze în ecuația de tangenta, este puțin probabil că va avea dificultăți cu construcția în planul este o linie dreaptă de la ecuația lui.
Noi folosim algoritmul de elaborare a ecuației de tangenta, dat fiind faptul că în acest exemplu, dar spre deosebire de exemplul anterior, aici există o incertitudine: nu este specificat în mod explicit abscisa punctului de tangență.
Începem să vorbim așa. Favorizate trebuie să fie paralelă cu linia tangentă y = 4-5. Două linii sunt paralele dacă și numai dacă acestea sunt coeficienți unghiulare. Prin urmare, panta liniei tangente trebuie să fie egală cu panta dreptei predeterminate: Astfel, valoarea unui putem găsi ecuația f „(a) = 4.
Avem:
Deci, din ecuație, există două tangente sarcină satisfăcătoare: unul la punctul cu abscisă 2, cealaltă la punctul cu abscisa -2.
Acum este posibil să funcționeze conform algoritmului.

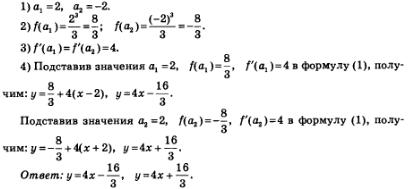
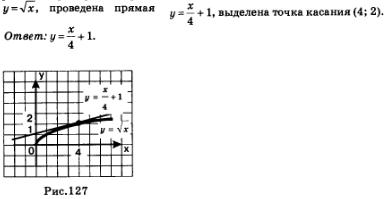
Exemplul 3. Din punctul (0, 1) tangenta la graficul
Decizie. Noi folosim algoritmul de elaborare a ecuației de tangenta, dat fiind faptul că în acest exemplu, rețineți că aici, la fel ca în exemplul 2, nu este specificat în mod explicit abscisa punctului de tangență. Cu toate acestea, noi acționăm pe algoritmul.

Prin tangent condiție trece prin punctul (0, 1). Substituind în ecuația (2) valorile lui x = 0, y = 1, obținem:
După cum puteți vedea, în acest exemplu, doar a patra etapă a algoritmului am reușit să găsim abscisa punctului de tangență. Substituind valoarea a = 4 în ecuația (2) randamentele:

Fig. 127 prezintă o ilustrare geometrică a exemplului de mai sus: funcția reprezentată grafic

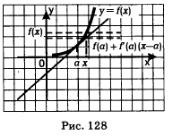
În § 32 am observat că funcția y = f (x), derivatul având o locație x fixă, următoarea ecuație aproximativă:

Pentru comoditatea de discuții suplimentare schimba notația: în loc de x si scriem, scriem în loc de x și, prin urmare, vom scrie în loc de x-o. Apoi, scris mai sus ecuația aproximativă devine:

Si uita-te acum la Fig. 128. La un grafic al funcției y = f (x) este realizată la un punct tangent M (a, f (a)). Marcat punct x pe abscisă și în apropiere. Este clar că f (x) - ordonata graficului punctul x specificat. Ce este f (a) + f „(a) (x-a)? Această tangentă ordonată corespunzătoare aceluiași punct x - vezi formula (1) .. Care este sensul egalității aproximativă (3)? Faptul că pentru calcularea valorii aproximative a unei funcții de a lua o valoare de tangenta ordonata.

Exemplul 4. Găsiți valoarea aproximativă a unei expresii numerice 1.02 7.
Decizie. Este vorba de a găsi valorile funcției y = x 7 x = 1.02. Folosind formula (3), ținând seama de faptul că, în acest exemplu
Ca rezultat, obținem:

Dacă vom folosi un calculator, obținem: 1.02 7 = 1.148685667.
După cum puteți vedea, precizia de aproximare este destul de acceptabil.
Răspuns: 1,02 7 = 1,14.

AG Mordkovich Algebra Grad 10

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.