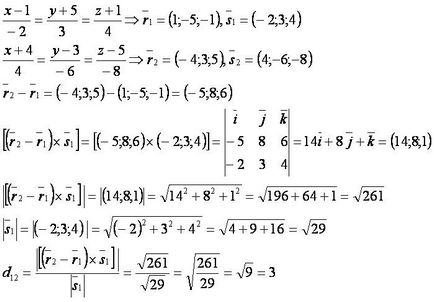Distanța dintre liniile drepte în spațiul tridimensional
[Math] \ bar r_1 = (x_1, y_1, z_1) [/ math] - vectorul raza unui punct de pe prima linie;
[Math] \ bar r_2 = (x_2, y_2, z_2) [/ math] - vectorul raza unui punct de pe a doua linie;
[Math] \ bar s_1 = (l_1, M_1, N_1) [/ math] - prima linie dreaptă vectorului;
[Math] \ bar s_2 = (l_2, m_2, n_2) [/ math] - un al doilea vector pe direcția dreaptă;
[Math] d _ [/ math] - distanța dintre prima și cea de a doua linie.
[Edit] Formula pentru liniile oblice
Pentru a înclina linii este dată de formula:
[Math] d _ = \ frac_2- \ overline_1 \ dreapta) \ overline_1 \ overline_2 \ dreapta |> _1 \ ori \ overline_2 \ dreapta] \ dreapta |> \ Leftrightarrow d _ = \ frac_2- \ overline_1 \ dreapta) \ cdot \ stânga [ \ overline_1 \ ori \ overline_2 \ dreapta] \ dreapta) \ dreapta |> _1 \ ori \ overline_2 \ dreapta] \ dreapta |> \ leftrightarrow [/ matematica] [matematica] \ leftrightarrow d _ = \ frac_2- \ overline_1 \ dreapta) \ ori \ overline_1 \ dreapta] \ cdot \ overline_2 \ dreapta) \ dreapta |> _1 \ ori \ overline_2 \ dreapta] \ dreapta |> \ leftrightarrow d _ = \ frac_2- \ overline_1 \ dreapta) \ overline_1 \ overline_2 >> _ 1 \ overline_2 >> [/ math]
Distanța dintre liniile oblice egal cu raportul dintre produsul mixt al modulului vectorilor (r2-R1), S1 și S2 la modulul produsului vectorial al vectorilor s1 și s2. Sensul geometric formula: lungime - este lungimea înălțimii paralelipipedului (formată din vectorii (r2-R1), s1 și s2), coborâtă la baza unui paralelogram (format prin vectorii s1 și s2), egală cu raportul dintre volumul la zona paralelipipedica paralelogram.
Formula distanța dintre liniile oblice sub formă de coordonate este:
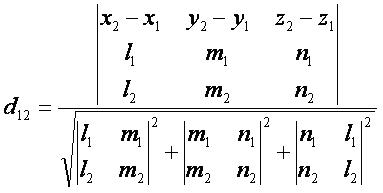
[Regula] EXEMPLUL
Luați în considerare două linii oblice: [matematica] \ frac = \ frac = \ frac [/ matematica] și [matematica] \ frac = \ frac = \ frac [/ matematică].
Găsiți distanța dintre ele.
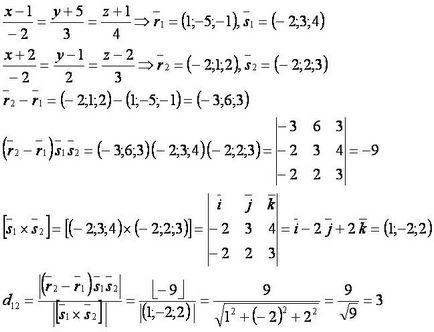
[Regula] Formula pentru linii paralele
Pentru linii paralele formula este:
Distanța dintre liniile paralele egale cu raportul dintre modulul produsului vectorial al vectorilor (r2 -R1) s1 și lungimea s1 vectorului. Sensul geometric formula: lungime - este lungimea înălțimii paralelogram (formată din vectorii (r2 -R1) și s1), a redus la baza paralelogramului ca vector (s1), care este egal cu raportul dintre aria paralelogramului lungimea bazei.
Formula distanței între liniile paralele într-o formă de coordonate este:
.
[Regula] EXEMPLUL
Găsiți distanța dintre ele.