Cum de a găsi zona acestui triunghi 1

16 (C4). Cunoscând zona de triunghiuri mari, în căutarea pentru o mică zonă (v. 83)

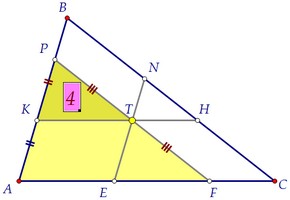
Prin punctul T trei k drepte a avut loc în interiorul triunghiului ABC, l și m astfel încât k || AB, l || BC, m || AC. Aceste linii formează un triunghi cu trei laturi ale unui triunghi, dintre care două sunt egale ca mărime. a) Să se arate că pătratul suma rădăcinilor pătrate ale zonelor triunghiurilor formate prin linii drepte k, l și m pe laturile triunghiului ABC. egală cu suprafața triunghiului; b) Găsiți zona triunghiului mai mic, în cazul în care se știe că treug zona. ABC este 25 și suprafața fiecăruia dintre triunghiuri congruente este 4.

Este clar că, dacă formula a) se dovedește, de a substitui în datele sale de la b) nu este dificil. Cu toate acestea decide în mod autonom b).

In triunghiuri din Figura laturile respectiv paralele între ele. Este ușor de a dovedi că acestea sunt similare în cele două colțuri. În cazul în care zonele de triunghiuri similare sunt egale, atunci triunghiuri sunt ele însele, de asemenea, egale (dovedesc).





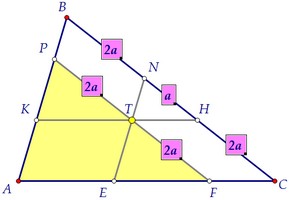
În triunghiuri egale, prin definiție, egal cu părțile relevante. Sărbătorim mai multe perechi de laturi egale, luând în considerare proprietățile unui paralelogram. Astfel, CT - APF linia mediană a triunghiului prin definiție. Zona APF a unui triunghi este de 4 ori mai mare decât suprafața triunghiului ABD. *** triunghiuri cu un factor de similaritate a doua. Triunghiuri APF și AVS asemanatoare. Zonele lor sunt 16 și 25. Acest lucru înseamnă că laturile corespunzătoare ale triunghiuri sunt 4. 5. Considerarea în același timp egalitatea de laturile opuse ale unui paralelogram: În cele din urmă, observăm încă o pereche de triunghiuri similare: KPT și TNH. Coeficientul de similitudine este egal cu 2. Aria medie de îngrijorare, ca 4 la 1. Astfel, suprafața triunghiului mic TNH este 1. Răspuns: 1 Dovedește afirmație a) este posibil, susținând în mod similar, desemnarea ariilor egale de date în ceea ce privește x. folosind aceeași asemănare și relațiile. Dar, pe pagina următoare se va dovedi într-o formă generală. adică, un punct arbitrar în interiorul triunghiului, prezența unor triunghiuri nu neapărat egale.