Cum de a excela pentru a rezolva un sistem de ecuații liniare - trucuri și tehnici în Microsoft Excel
În acest articol, vă vom arăta cum să utilizați formula pentru sistemele de ecuații liniare de rezolvare.
Aici este un exemplu al unui sistem de ecuații liniare:
3x + 4y = 8
4x + 8y = 1
Soluția este de a găsi astfel de valori ale lui x și y. care satisfac ambele ecuații. Acest sistem de ecuații are o singură soluție:
x = 7,5
y = -3625
Numărul de variabile într-un sistem de ecuații trebuie să fie egal cu numărul de ecuații. Exemplul anterior utilizează două ecuații cu două variabile. Sunt necesare trei ecuații pentru a găsi valorile celor trei variabile (x, y și z). Acțiuni comune pentru sistemele de ecuații de rezolvare după cum urmează (Fig. 128.1).
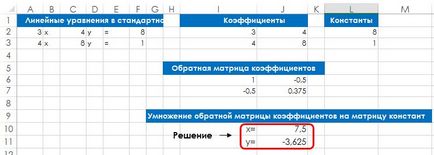
Fig. 128,1. Folosind formula de rezolvare a unui sistem de două ecuații
- Se exprimă ecuația în formă standardizată. Dacă este necesar, utilizați elementele de bază ale algebrei și rescrie ecuația, astfel încât toate variabilele sunt afișate în partea stângă a semnului egal. Următoarele două ecuații sunt identice, dar al doilea este dat în formularul standard:
3x - 8 = -4y
3x + 4y = 8. - Fii rapoarte în intervalul de dimensiune a ochiurilor n x n. unde n reprezintă numărul de ecuații. Fig. 128,1 rapoarte sunt în intervalul I2: J3.
- Se pune o constantă (numerele de la dreapta semnului egal) în intervalul verticală a celulelor. Fig. 128.1 constante sunt în gama L2: L3.
- Utilizați formule matrice pentru calculul coeficienților matricei inverse. Fig. 128.1 Următoarea formulă a fost pus în gama matrice I6: J7 (nu uitați să apăsați Ctrl + Shift + Enter pentru a introduce formula matrice.): = ASI (I2: J3).
- Utilizați o formulă matrice pentru multiplicarea coeficienților matricei inverse ale matricei de constante. Fig. 128.1 Următoarea formulă matrice introdusă în gama J10: JJ11. care conține soluția (x = 7,5 și y = -3.625) = MMULT (I6: J7 L2: L3). Fig. 128.2 prezintă o foaie care este configurată pentru a rezolva sistemul de trei ecuații.
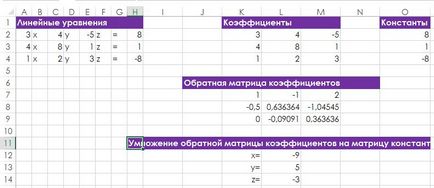
Fig. 128,2. În Excel, puteți rezolva un sistem de trei ecuații, aplicând formula dorită