Cercetarea în geometria matematică a cercurilor

Continuarea calcul până la 3072-gon, el a găsit o aproximare mai precisă la o fracție zecimală este egală cu 3,14159.

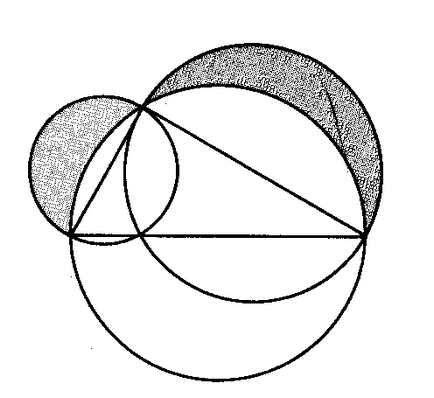
Pe laturile unui triunghi dreptunghic ca diametru în afara semicercuri construite. Dovedește că zona semicercului, construit pe ipotenuzei este egal cu suma suprafețelor de semicercuri, construit pe Catete.

Arătăm că S = S1 + S2. Să unul dintre picioarele unui triunghi dreptunghic este egal cu x, iar celălalt picior este, atunci ipotenuzei este egal cu teorema lui Pitagora

Găsiți S1. Deoarece S2 și S. raza primului cerc este egal cu x / 2 și raza celui de al doilea cerc este egal cu y / 2, iar raza celui de al treilea cerc este,

S1 + S2 = + =. QED.
Problema № 2.

Având în vedere un pătrat cu laturile egale 1. Găsiți zona figura umbrită.

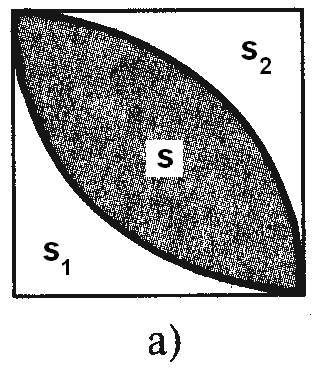
Soluție: Să ne găsim o zonă pătrat: S = 1.

Zona S + S1 = ¼ pătrat raza cercului egal cu 1.

Găsim zona ¼ cerc: S + S1 = / 4

Zona Naodom S2 = suprafața unui pătrat - zona S + S1

Pentru a găsi zona figura umbrită, se scade suprafața unui pătrat de suprafață S1 și S2. Obținem: S = 1-2 (1/4) = 1-2 + / = 2 / 2-1.

Arc circumscris cercuri, poligoane regulate delimitează lateral, sunt afișate simetric în raport cu aceste laturi. Caută:

1) Zona de forme umplute dacă latură a poligonului este egal cu 1;

2) Găsiți suprafața unei forme asemănătoare cu un pentagon regulat; n dreapta - gon.

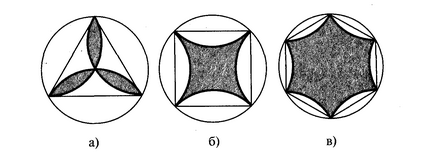
Răspuns: 1) Zona figura trohlepestkovoy este diferența dintre suprafața segmentului circular triple și zona de triunghi. De trei ori suprafața unui segment circular egal cu diferența dintre suprafața cercului și aria triunghiului. Astfel, suprafața necesară este egală.

2) Suprafața cifra umbrită egală cu diferența dintre dublul ariei poligonului și zona de cerc.

oh

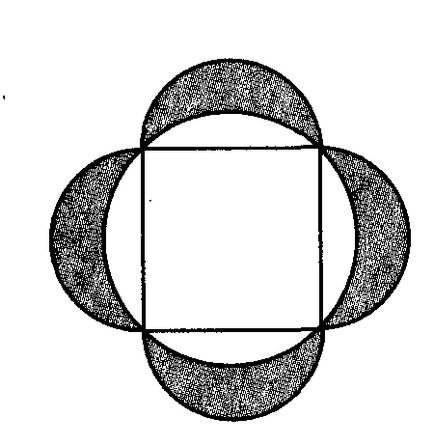
pătrat Kolo cu partea 1 a descris un cerc, iar pe laturile sale ca diametru semicercul construit. Găsiți zona figura umbrită.
Răspuns: 1.

P

Ostrow trei arce de cerc cu centre și se termină cu o latură a unui triunghi echilateral topuri 1. Găsiți zona de forma rezultată.

H

și laturile a, b, un triunghi dreptunghic în diametrul cercului construit. Găsiți zona figura umbrită.

răspundă:

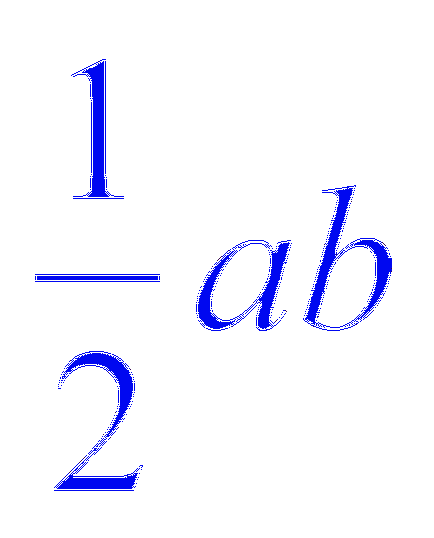
WAdachi № 7.

Diametrul 2R Circumferința împărțit în patru segmente egale. La primirea segmentelor sunt construite semicerc. Se calculează aria de forme pline. Calculeaza lungimea fiecărei forme de contur umbrite.

W

acolo cercuri de egale cu raza R ating cercul aceeași rază și în perechi unul de altul. În ceea ce privește inelul de șase cercuri, iar aria sa este aria celor șapte cercuri de date. Găsiți lățimea inelului.

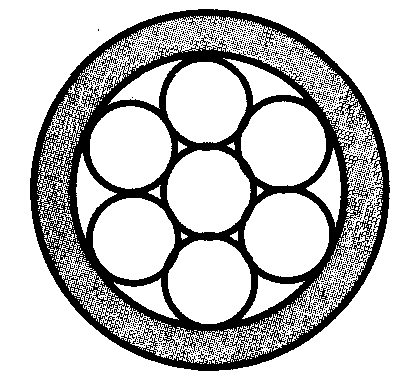
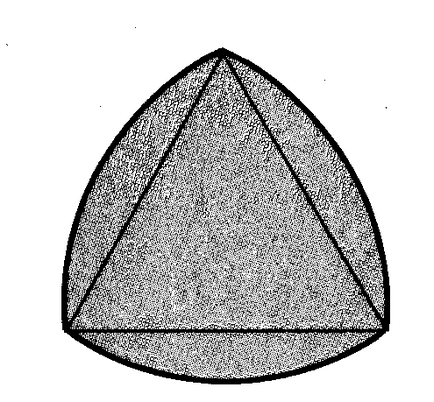
Trei cercuri egale se ating și raza cercului R. găsi raze lor. Rezolva această problemă pentru patru, cinci, opt cercuri.

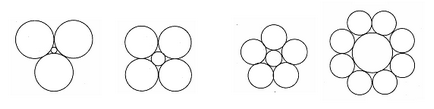
Răspuns: Raza cercului x poate fi găsit din ecuația , unde n - numărul de cercuri.

triunghi cerc înscris de tangentele rază r paralele cu laturile triunghiului. Triunghiurile retezate tangentele inscripționate cerc raze R1, R2 și R3. Demonstrati ca r1 + r2 + r3 = r.

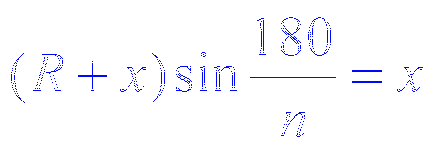
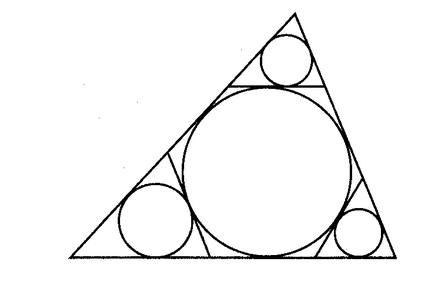
Mental efectua această procedură cu fiecare dintre cele trei triunghiuri tăiate, și așa mai departe. D. Găsiți suma razelor cercurilor care rezultă în fiecare etapă.

Răspuns: Dacă ha. hb. hc - înălțimea triunghiului, înălțimile respective ale triunghiuri mici vor fi egale, ha -2R, hb -2R, hc -2R. Din similitudinea triunghiuri localiza această sumă de relații, înlocuindu-le cu raportul de înălțime.

Cercetare în Matematică Tema: „Magic Triangle“