Ce este covarianța
O relație caracteristică între variabilele aleatoare X și Y este așteptarea funcționează X și Y abateri ale centrelor de distribuțiile lor (denumite uneori speranța matematică a unei variabile aleatoare) se numește coeficientul de covarianță sau pur și simplu covarianță.
Această formulă poate fi interpretat după cum urmează. În cazul în care pentru valori mari ale lui x sunt valori mai probabil mai mari Y, și la valori mici ale lui X sunt valori mai probabil mici Y, atunci partea dreapta a covarianța termeni pozitivi domină, iar covarianța ia valori pozitive.
Dacă produsul mai probabil (xi - EX) (yj - EY), constând din factorii de semne opuse, adică rezultatul unui experiment de plumb aleatoriu la valori mari ale lui X rezultat, în general valori mici ale lui Y și invers, covarianța primește negativ mare absolută valori.
În primul caz, se obișnuiește să se vorbească de comunicare directă: ca o variabilă aleatoare X Y tinde să crească.
În al doilea caz vorbim despre feedback-ul: ca variabila aleatoare X Y are o tendință de scădere sau să cadă.
Dacă aproximativ aceeași contribuție în valoarea randamentului atât produs pozitiv și negativ (xi - EX) (yj - EY) pij. putem spune că împreună vor „stinge“ unul pe altul, iar covarianța va fi aproape de zero. În acest caz, nici o dependență vizibilă a unei variabile aleatoare a celuilalt.
Este ușor de a arăta că, dacă
Într-adevăr, din (2)
Aici am folosit o proprietate foarte importantă a așteptărilor: așteptarea unei abateri variabile aleatoare de la așteptările sale matematice este egală cu zero.
Covarianță prezentate convenabil sub formă de
Covarianța două variabile aleatoare este egală cu așteptarea produsului lor minus produsul așteptărilor.
În ceea ce privește variabilele independente exy = EXEY, este evident că pentru independente aleatoare variabile X și Y cov (X, Y) = 0.
Definiția. Variabilele aleatoare, covarianța este zero, numit necorelate.
.Notă. Așa cum sa arătat mai sus, de la independența variabilelor aleatorii care trebuie să le necorelate, care este egal cu zero, corelație. Reciproca nu este adevărat! Să considerăm un exemplu adecvat:
Lăsați variabila aleatoare X are o distribuție uniformă pe intervalul (-1, 1) și aleatoare Y variabilă este asociat cu variabila X relație funcțională aleatoare Y = X 2. Vom arăta că cov (X, Y) = 0, cu toate că există o relație funcțională.
Având în vedere. că EX = 0 (mijlocul intervalului (-1,1)), obținem:
cov (X, Y) = exy-EXEY = EX = 3
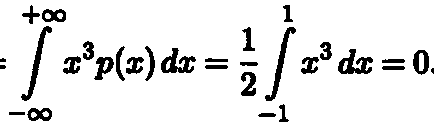
Deci, de variabile aleatoare necorelate nu ar trebui să fie independența.
Covarianță valori aleatoare reflectă gradul de dependență al variabilelor aleatoare de proximitate la liniar, adică, o dependență de forma Y = AXE + b.
Să considerăm acum o altă măsură de dependență liniară - coeficientul de corelare a variabilelor X și Y r (X, Y) aleatoare =
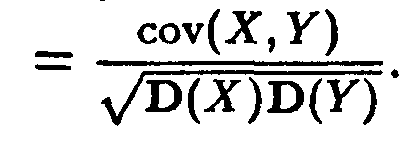
Problema poate apărea, de ce introduce o altă măsură de dependență liniară?
Coeficientul de corelație variază între -1 la 1, în loc de întreaga axă reală
Coeficientul de corelație, spre deosebire de covarianța insensibil la unitățile de schimbare
În cazul în care variabilele aleatoare sunt independente, coeficientul de corelație ca covarianța este zero.
Dacă valoarea aleatorie este dependentă liniar, apoi r = 1 - o relație directă. r = -1, invers. Și invers, de egalitate modulo 1 ar trebui să fie o relație liniară.
Să distribuția variabilelor aleatoare de masă specificate
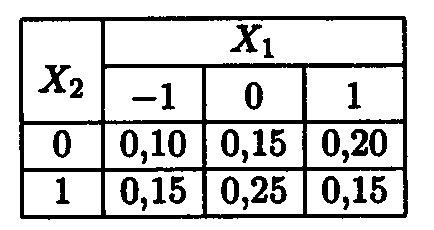
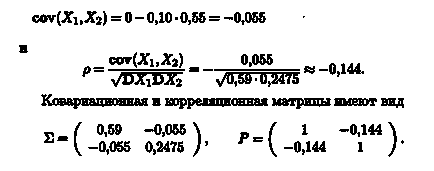
Notă. Covarianță și corelarea matricei - un tabel, respectiv, coeficienții de corelație covarianță și variabile aleatoare corespunzătoare. (Rețineți că diagonala principală a matricei de corelare sunt 1 - variabile aleatoare, evident cu ea însăși este o funcție liniară). Utilizați aceste matrici pentru a vizualiza relația dintre valorile de date și statistici.