Calculul suprafeței din cifra indicată pe hârtie grafic
În pregătirea pentru examenul de stat de bază, am întâlnit cu sarcini care necesită calcula aria figurii prezentate într-o foaie de hârtie în carouri. De regulă, aceste sarcini nu provoacă mari dificultăți, în cazul în care cifra este un trapez, paralelogram sau un triunghi. suficient de bine pentru a cunoaște formulele de calcul domeniile acestor cifre și se numără numărul de celule pentru a calcula zona. În cazul în care cifra este un poligon arbitrar, este necesar de a utiliza tehnici speciale. Am fost interesat de acest subiect. Și, desigur, orice întrebări: în cazul în care în viața cotidiană poate fi o problemă în calcularea zonelor pe hârtie grafic? Ce este special cu privire la aceste probleme? Există și alte metode sau o formulă universală pentru calcularea suprafeței figurilor geometrice reprezentate pe hârtie milimetrică?
Având în vedere un sistem de coordonate rectangular. Considerăm un poligon care are coordonate întregi în acest sistem. În punctele de literatură academice cu coordonate întregi sunt numite noduri. Iar poligonul nu trebuie să fie convexă. Și să fie necesar să se determine zona sa.
Următoarele cazuri.
1. Cifra este un triunghi, paralelogram, trapez:
1) celule de numărare trebuie să găsească înălțimea, diagonală sau părți care sunt necesare pentru a calcula suprafața;
2) substituie valoarea găsită în formula zonă.
De exemplu, este necesar să se calculeze aria figurii prezentate în Figura 1 la dimensiunea celulelor 1cm 1cm.
Fig. 1. Triunghiul
Decizie. Contăm celulele și pentru a găsi că. Conform formulei obținem :.
Figura 2 este un poligon
Dacă forma este un poligon este posibilă utilizarea următoarelor metode.
1) împart poligon în triunghiuri, dreptunghiuri;
2) se calculează cifrele zonei obținute;
3) Găsiți suma tuturor zonelor de forma rezultată.
De exemplu, este necesar să se calculeze aria figurii prezentată în figura 2, cu o dimensiune a celulei de 1cm de 1cm partiție.
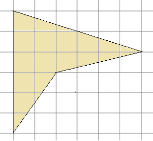
Fig. 2. Poligon
Decizie. Partition, există mai multe moduri. Impartim figura în triunghiuri unghi drept și un dreptunghi așa cum se arată în figura 3.
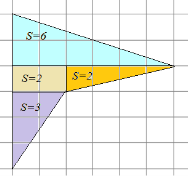
Fig. 3. Poligon. metoda de partiționare
Zonele de triunghiuri sunt egale: ,,, aria dreptunghiului -. aria tuturor cifrelor pe care le primim Folding:
Metoda de construcție a suplimentare
1) pentru a termina forma unui dreptunghi
2) pentru a găsi zona a primit cifre suplimentare și aria dreptunghiului
3) din suprafața dreptunghiului pentru a scădea aria tuturor pieselor „extra“.
De exemplu, este necesar să se calculeze aria figurii prezentată în figura 2, cu o dimensiune a celulei de 1cm prin 1cm construcție suplimentară.
Decizie. Vom termina forma noastră la un dreptunghi așa cum se arată în figura 4.
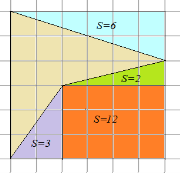
Fig. 4. Poligon. metoda adăugări
Zona dreptunghiului de mare este egal cu dreptunghiului localizat în interiorul -, zona de triunghiuri „extra“ -, atunci suprafața dorită a figurii.
La calcularea zona poligoane pe hârtie carouri posibil să se utilizeze o altă metodă, care este cunoscut sub numele de Teorema lui Pick pe numele cercetătorului care a descoperit-o.
Să poligonului reprezentate pe grafic hârtie numai vertex întreg. Momentul în care ambele coordonate sunt numere întregi numite site-uri cu zăbrele. Mai mult decât atât, poligonul poate fi fie convex sau non-convexe.
zona unui poligon cu vârfuri întregi egale în cazul în care B - numărul de puncte întregi în interiorul poligonului și F - numărul de puncte întregi pe conturul poligonului.
De exemplu, pentru poligon ilustrat în figura 5.
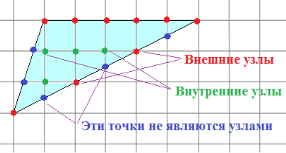
Fig. 5. Nodurile în formula Peak
De exemplu, este necesar să se calculeze aria figurii prezentată în Figura 2 cu dimensiunea celulelor 1cm 1cm formula Peak.
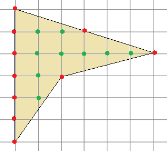
Fig. 6. Poligon. Teorema lui Pick
Decizie. Conform figurii 6: In = 9, T = 10, atunci avem formula Peak:
1. Copiii de grădiniță făcut cerere părinților ca prezent (Figura 7). Localizați zona de aplicare. Mărimea fiecărei celule este de 1 cm 1sm.
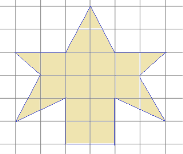
Fig. 7. Condiția Problema 1
2. Un hectar de standuri de molid poate întârzia un an la 32 de tone de praf, pin - până la 35 de tone, ulm - până la 43 de tone de stejar - pana la 50 de tone de fag - .. Count cu până la 68 de tone cât de multe tone de praf brad întârziere de 5 ani. Planul de molid este prezentat în Figura 8 (o scară de la 1 cm -.. 200 m).
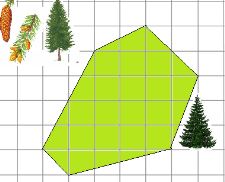
Fig. 8. Condiția Problema 2
3. ornamente Hanti și Mansi, dominat de motive geometrice. De multe ori există imagini stilizate de animale. Figura 9 prezintă un fragment Mansiysk ornament „urechi iepuras“. Se calculează aria părții umbrită a ornament.
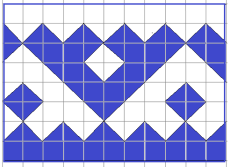

Fig. 9. Condiția Problema 3
4. Necesar pentru a picta pereții clădirii fabricii (fig. 10). Se calculează cantitatea necesară de vopsele latex (în litri). Debitul de cerneală: 1 litru 7 mp. metru scara 1cm - 5m.
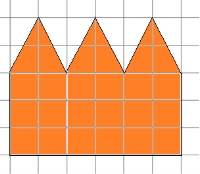
Fig. 10. Condiția 4 Problemă
5. poligon stelat - figura geometrică plană compusă din raze triunghiulare care provin dintr-un centru comun, care fuzionează într-un punct de convergență. O atenție specială ar trebui să fie cinci colțuri stele - pentagramă. Pentagrama - un simbol de excelență, inteligență, înțelepciune și frumusețe. Aceasta este cea mai simplă formă de stele, care pot fi reprezentate printr-o singură trăsătură de condei, nu-l scoate din hârtie și, astfel, nu același lucru, fără a trece de două ori pe aceeași linie. Desenați o stea cu cinci colțuri, fără a ridica creionul de pe foaia de hârtie milimetrică, astfel încât toate colțurile poligonului rezultat este în nodurile de celule. Se calculează aria figurii obținute.
După analiza literaturii matematice și sortați un mare număr de exemple pe subiectul cercetării, am ajuns la concluzia că alegerea metodei de calcul din zona unei figuri pe o hârtie în carouri depinde de forma a figurii. În cazul în care forma este un triunghi, dreptunghi, paralelogram sau un trapez, este convenabil pentru a profita de toate cunoscute formulele de calcul a zonelor. Dacă forma este un poligon convex, atunci este posibil să se utilizeze ca metodă de partiționare și add-on (în cele mai multe cazuri, este mai convenabil - metoda adăugări). Dacă cifra este un poligon non-convex, sau în formă de stea, care este mai convenabil să se aplice cu formula Vf.
Deoarece formula Vârful este o ecuație universală pentru calcularea zonelor (în cazul în care vârfurile poligonului sunt la punctele de zăbrele), acesta poate fi folosit pentru orice figură. Cu toate acestea, în cazul în care un poligon ocupă o suprafață mare (sau cu celule mici), atunci este probabil să facă o greșeală în numărarea nodurile zăbrele. În general, în cursul cercetării, am ajuns la concluzia că, în a face cu astfel de probleme în JEG mai bine să se folosească metode tradiționale (divizare sau add-on), iar rezultatul este verificată de formula Peak.
