Zona de cerc
Cercul necesită o abordare mai atentă și să apară mult mai puține locuri de muncă B5. Cu toate acestea, soluțiile generale schema chiar mai ușor decât în cazul poligoane (a se vedea. Lecția „pătrate poligoane pe grila“).
Tot ceea ce este necesar în aceste sarcini - raza de căutare R. zona circumferențială a unui cerc poate fi calculată apoi de formula S = πR 2. De asemenea, din această formulă, care este suficient pentru a găsi soluții pentru R2.
Pentru a găsi aceste valori, este suficient să cerc un punct care se află la intersecția liniilor de grilă. Și apoi utilizați teorema lui Pitagora. Luați în considerare exemplele specifice de calcul a razei:
Sarcină. Găsiți razele de cele trei cercuri prezentate în figură:

Execută construcții suplimentare în fiecare cerc:
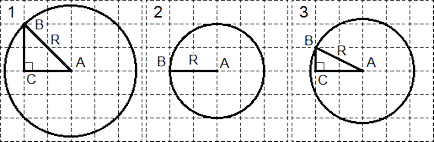
In fiecare caz, este selectat punctul B de pe circumferință, astfel încât să se afle la intersecția liniilor de grilă. Punctul C în cercurile 1 și 3 sunt complementare forma unui triunghi dreptunghiular. Rămâne de a găsi razele:
Luați în considerare triunghiul ABC în primul cerc. Prin Teorema pitagoreic: R2 = AB 2 = AC + BC 2 = 2 2 2 + 2 2 = 8.
Pentru toate, evident, al doilea cerc: R = AB = 2.
Al treilea caz este similar cu primul. Din triunghiul ABC teorema lui Pitagora: R2 = AB 2 = AC + BC 2 = 1 2 2 + 2 2 = 5.
Acum știm cum să găsească raza unui cerc (sau cel puțin pătrat acestuia). Și, prin urmare, putem găsi zona. Există sarcini care necesită acest sector pentru a găsi zona, mai degrabă decât întreaga gamă. În astfel de cazuri, este ușor să dau seama ce o parte din termenii acestui sector, și, astfel, pentru a găsi zona.
Sarcină. Găsiți zona de S a sectorului umbrit. În răspunsul dvs., S / π.
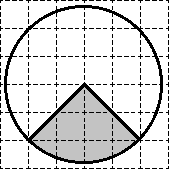
Evident, sectorul reprezintă un sfert de cerc. În consecință, S = 0,25 · S cerc.
Rămâne de a găsi o serie de S - suprafața unui cerc. Pentru a face acest lucru, efectuați construcții suplimentare:
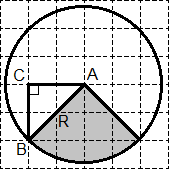
Dreptunghiular - ABC triunghi. Prin teorema lui Pitagora, avem: R2 = AB 2 = AC + BC 2 = 2 2 2 + 2 2 = 8.
Acum ne găsim aria unui cerc și sectoare: cerc S = πR 2 = 8 π; S = 0,25 · S cerc = 2 π.
În final, valoarea dorită este egală cu S / π = 2.
Zona sectorului la o rază necunoscută
Vestea bună este că astfel de probleme - cea mai simplă a tuturor sarcinilor în domeniile care sunt în examenul la matematică. În plus, cercul și sectorul este întotdeauna plasat pe grătar. Prin urmare, pentru a afla cum să rezolve astfel de probleme, doar uita-te la poza:

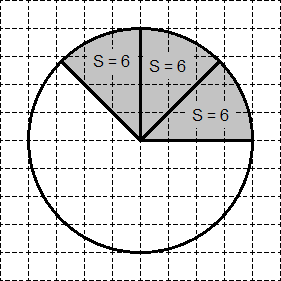
Să presupunem că cercul inițial are o suprafață S = roata 80. Apoi, ea poate fi împărțită în două sectoare, o suprafață S = 40 fiecare (vezi. Etapa 2). In mod similar, fiecare dintre aceste „jumătăți“ sektorov- poate fi împărțit în jumătate din nou - obține patru sectoare S = 20 fiecare zonă (vezi pasul 3). În cele din urmă, este posibil să se împartă fiecare dintre aceste sectoare pentru două - obține 8 sektorov- „bulgări“. Suprafața fiecăreia dintre aceste „bulgărilor“ va fi S = 10.
Notă: o partiție mică de orice problemă examenul la matematică nu este! Astfel, algoritmul pentru B-3, după cum urmează:
- Se taie cercul inițial în 8 sektorov- „bulgări“. Suprafața fiecăreia dintre ele este exact 1/8 din suprafața întregului cerc. De exemplu, în cazul în care starea roții are o zonă circulară S = 240, atunci „smocuri“ sunt S = 240. 8 = 30 suprafață;
- Aflați cât de multe „resturi“ este plasat în sectorul inițial al zonei pe care doriți să căutați. De exemplu, în cazul în care sectorul nostru este plasat 3 „bucăți“ de 30, zona dorită a sectorului este egal cu S = 3 x 30 = 90. Acesta va fi răspunsul.
Asta este! Problema este rezolvată aproape în mod verbal. Dacă încă nu înțeleg ceva, cumpara o pizza si se taie in 8 bucati. Fiecare piesă ar sektorom- astfel „bulgări“, care ar putea fi combinate în bucăți mai mari.
Și acum, uita-te la un eșantion de examen de testare:
Sarcină. Pe hârtie milimetrică desena un cerc a cărui suprafață este egală cu 40. Găsiți zona figura umbrită.
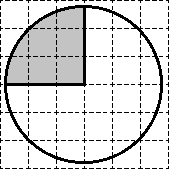
Astfel, suprafața unui cerc este egal cu 40. împarte în 8 sectoare - fiecare arie S = 40. 5 = 8. obține:
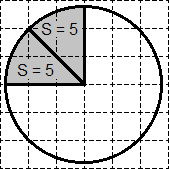
În mod evident, sectorul hașurată este format din exact două sektorov- „resturi“. În consecință, o suprafață egală cu 2 · 5 = 10. Asta e tot o soluție!
Sarcină. Pe hârtie milimetrică desena un cerc a cărui suprafață este egală cu 64. Găsiți zona figura umbrită.
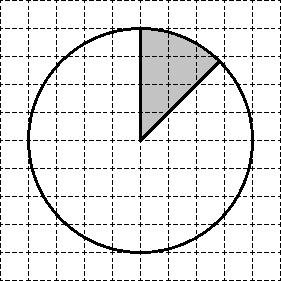
împărți din nou întregul cerc în 8 sectoare egale. Este clar că zona unuia dintre ei doresc doar să găsească. Prin urmare, suprafața sa este S = 64. 8 = 8.
Sarcină. Pe hârtie milimetrică desena un cerc a cărui suprafață este egală cu 48. Găsiți zona figura umbrită.
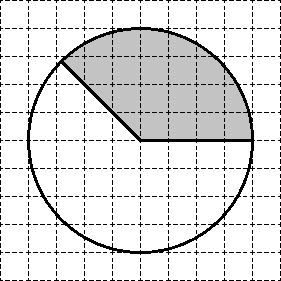
împărțiți din nou cercul în 8 sectoare egale. Suprafața fiecăreia dintre ele este egală cu S = 48. 8 = 6. În sectorul solicitat este plasat exact trei „bucăți“ sektora- (vezi. Figura). Prin urmare, suprafața sectorului dorit este 3 x 6 = 18.
- Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
