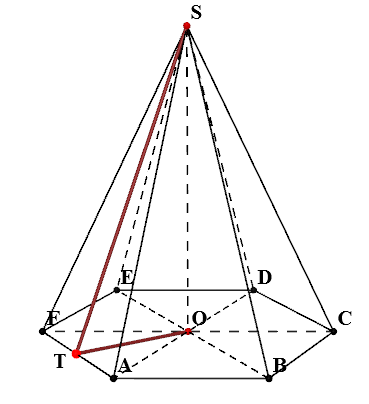
Regular piramidă hexagonală Bank CSE

piramidă hexagonală regulată - o piramidă a cărei bază este un hexagon regulat.

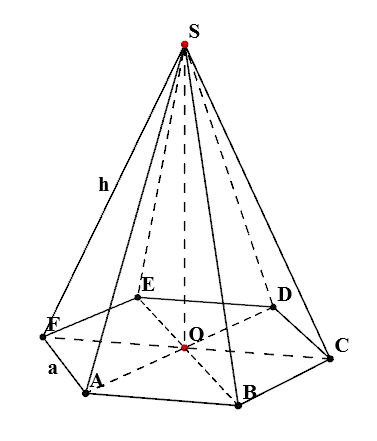
denumiri

• $ SABCDEF $ - piramida hexagonala regulate
• $ O $ - de bază centrul piramidei
• $ A $ - lungime laterală a bazei piramidei
• $ H $ - lungimea marginilor laterale ale piramidei
• $ S _> $ - baza pătrată a piramidei
• $ V _> $ - volumul piramidei

Suprafața bazei piramidei

La baza piramidei este un hexagon regulat cu laturi $ a $. Conform proprietăților unui hexagon regulat, baza pătrată a piramidei este egal cu S $$ _> = \ frac> \ cdot a ^ 2 $$

hexagon regulat în partea de jos a piramidei

Conform proprietăților unui hexagon regulat, triunghiuri AOB, BOC, COD, DOE, EOF, FOA sunt triunghiuri drepte. Rezultă că $$ AO = OD = EO = OB = CO = = unui fir $$ tăiat AE, se intersectează cu CF segment la isoscel M. AEO Triangle, există $ AO = OE = a, \ \ unghiul EOA = $ la 120 ^. Conform proprietăților unui triunghi isoscel $$ AE = a \ cdot \ sqrt = \ sqrt \ cdot un $$ În mod similar, putem concluziona că $ AC = CE = \ sqrt \ cdot un $, $ FM = MO = \ frac \ cdot un $.

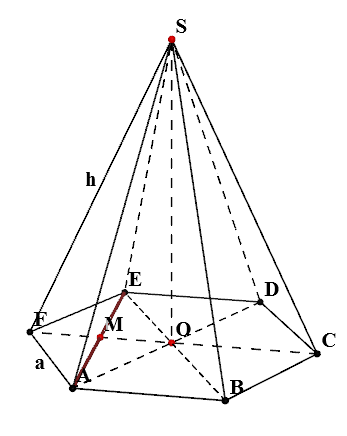
Găsiți $ $ SO

Direct de SO $ $ este înălțimea piramidei, deci $ \ unghi FPS = 90 ^ $. FPS triunghi $ $ dreptunghiular, în ea $ FO = a, \ FS = h $. Conform proprietăților unui triunghi dreptunghic $$ SO = \ sqrt = \ sqrt $$

Volumul piramidei

Volumul piramidei este calculat ca o treime din suprafața produsului său de bază la înălțimea sa. Înălțimea unei piramide regulate este tăiat $ SO $. La baza prismă hexagonală regulată este un hexagon regulat, o zonă cunoscută pentru noi. Se obține $$ V _> = \ frac \ cdot S _> \ cdot SO = \ frac> \ cdot a ^ 2 \ cdot \ sqrt $$

ST găsi $ $ $ și la $

Să punctul $ T $ este punctul de mijloc al nervurilor $ AF $. Triangle $ $ AOF corecta, prin urmare, proprietățile unui triunghi echilateral $$ TO = \ Frac> \ cdot un triunghi $$ STO $ $ dreptunghiul, înălțimea de SO $ $ este de $ \ sqrt $. Prin teorema lui Pitagora $$ ST = \ sqrt = \ sqrt \ cdot a ^ 2> $$