Rădăcinile unei ecuații pătratice

Formula rădăcini ecuație pătratică. Cazurile de rădăcini reale, multiple și complexe. Factoring polinom pătratic. Interpretarea geometrică. Exemple de determinare a rădăcinilor și factorizations.

formula de bază

Luați în considerare ecuația de gradul doi:
(1).
Rădăcinile ecuației pătratice (1) determinat prin formulele:
;.
Aceste formule pot fi combinate după cum urmează:
.
Când sunt cunoscute rădăcinile ecuației pătratice, atunci polinomul de gradul al doilea poate fi reprezentat ca un produs de factori (factored):
.

În continuare, considerăm că - numerele reale.
Luați în considerare discriminantul ecuației pătratice:
.
Dacă discriminantul este pozitiv. ecuația de gradul doi (1) are două rădăcini reale distincte:
;.
Apoi, extinderea factorizării polinomiale pătratic este de forma:
.
În cazul în care discriminant este zero. ecuația de gradul doi (1) are două multiple (egale) rădăcini reale:
.
factoring:
.
Dacă discriminantul este negativ. ecuația de gradul doi (1) are două rădăcini complexe conjugate:
;
.
Aici - unitatea imaginară;
și - părțile reale și imaginare ale rădăcinilor:
;.
atunci

interpretare grafică

Dacă vă construi un grafic al funcției
.
care este un parabole, punctul grafic de intersecție cu axa va fi rădăcini ale ecuației
.
Când. grafic intersectează abscisa (axa) în două puncte.
Când. În ceea ce privește grafic axa absciselor la un moment dat.
Când. Graficul intersectează abscisa.

Următoarele sunt exemple de astfel de grafice.

Formulele utile legate de o ecuație pătratică

Derivarea ecuației pătratice pentru rădăcinile

Noi efectua conversia și utilizarea formulei (F.1) și (F.3):

Astfel, avem formula pentru un polinom de gradul al doilea în formă de:
.
Acest lucru arată că ecuația

se efectuează la
și.
Adică, sunt rădăcinile unei ecuații pătratice
.

Exemple de determinare a rădăcinilor ecuației pătratice

Găsiți rădăcinile ecuației pătratice:
(1.1).

Scriem ecuația de gradul doi în forma generală:
.
Comparând cu ecuația noastră (1.1), găsim valorile coeficienților:
.
Găsim discriminante:
.
Deoarece discriminant este pozitiv. atunci ecuația are două rădăcini reale:
;
;
.

De aici obținem descompunerea factoringului polinom pătratic:

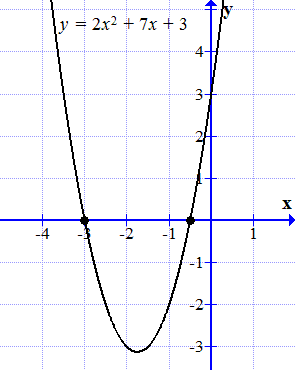
Graful y = x 2 + 7 x 2 + 3 intersectează axa orizontală în două puncte.

Noi construim graficul funcției
.
Graficul acestei funcții este o parabolă. Se subculturi abscisă (axa), la două puncte:
și.
Aceste puncte sunt rădăcinile ecuației inițiale (1.1).

Găsiți rădăcinile ecuației pătratice:
(2.1).

Scriem ecuația de gradul doi în forma generală:
.
Comparând cu ecuația inițială (2.1), descoperim valorile coeficienților:
.
Găsim discriminante:
.
Deoarece discriminant este zero. atunci ecuația are două Root multiple (egale):
;
.

Apoi, expansiunea factoring trinom este după cum urmează:
.

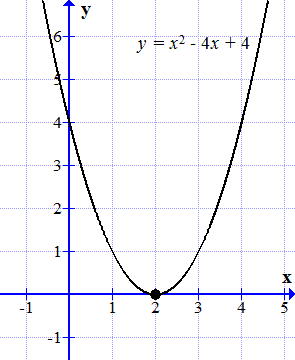
Graful y = x 2 - 4 x + 4 se referă la abscisă la un punct.

Noi construim graficul funcției
.
Graficul acestei funcții este o parabolă. Aceasta se referă la abscisa (axa), la un moment dat:
.
Acest punct de pornire este o rădăcină a ecuației (2.1). Deoarece această rădăcină este parte factoring sunt de două ori:
.
atunci o astfel de rădăcină se numește multiple. Asta este, considerăm că există două rădăcini egale:
.

Găsiți rădăcinile ecuației pătratice:
(3.1).

Scriem ecuația de gradul doi în forma generală:
(1).
Rescriem ecuația originală (3.1):
.
Comparativ cu (1), găsim valorile coeficienților:
.
Găsim discriminante:
.
Discriminant este negativ. Prin urmare, nu există nici rădăcini reale.

Puteți găsi rădăcini complexe:
;
;
.

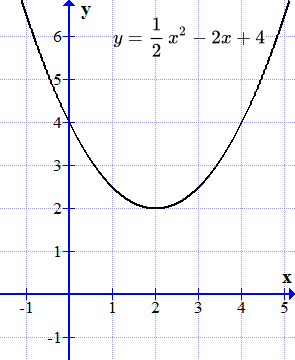
Funcția Program intersectează axa x. Nu există rădăcini reale.

Noi construim graficul funcției
.
Graficul acestei funcții este o parabolă. Ea nu traversează axa x (axa y). Prin urmare, nu există nici rădăcini reale.

Nu există rădăcini reale. Rădăcinile complexului:
;
;
.