metode de proiecție

Pentru afișarea punctului original în desenul este utilizată funcționarea de proiecție. Există un plan de proiecție (uneori numit un plan de imagine), în care se obține imaginea originală - proiecția punctului A. Operația constă în realizarea, prin punctul A al liniei drepte, care se numește proeminentă.

A1 Point - punctul de intersecție cu planul P1- drepte proeminent numit proiecția punctului A pe planul P1.

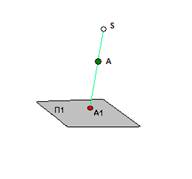
Desene, construite prin metoda de proiecție se numește proiecție.

În funcție de poziția de proiecție a razelor proeminente poate fi fie central (conice) sau paralele (cilindrice).

Atunci când se proiectează un obiect complex care se proiectează fiecare punct.

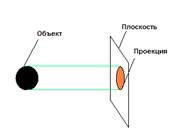
Cel mai frecvent caz de a primi proiecții figuri spațiale - este proiecția centrală.

În acest caz, grinzile proeminente în curs de dezvoltare de la un singur punct - centrul de proiecție S, care se află la o distanță finită de planul de proiecție P1.

Pentru a primi proiecția centrală a punctelor A și B, trebuie să se proiectează razele din centrul de proiecție S prin punctele A și B la P1 intersecție cu planul de proiecție. Când se obțin punctele de intersecție A1 și B1 - proiecția centrală a punctelor A și B.

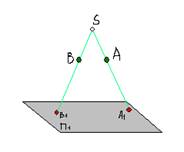
Poziția punctului S și planul P1. care nu trece prin centrul de proiecție, unitatea centrală determină proiecția. Dacă este setat, atunci putem determina întotdeauna poziția de orice punct al spațiului de proiecție centrală pe planul de proiecție, în care fiecare punct în spațiu va avea doar o singură proiecție centrală. Cu toate acestea, una dintre proiecția centrală este imposibil să se determine poziția unui punct în spațiu, deoarece poate fi oriunde în linie care leagă proiecția punctului și centrul de proiecție.

Pentru a determina poziția punctului A în spațiul de pe proiecția centrală trebuie să aibă două proiecții centrale ale acestui punct A1 și A2 sunt derivate din două puncte diferite S1 și S2. Dacă vom trage razele proeminente S1A1 și S2A2, punctul lor de intersecție determină în mod clar poziția punctului A în spațiul.

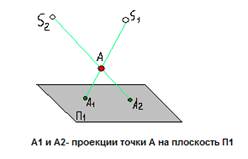
Pentru a construi segmentul de proiecție a1b1 centrală AB este suficient pentru a construi proiecțiile centrale A1 și B1 punctele A și B, deoarece cele două puncte definesc în mod unic o linie dreaptă.

Proiecțiile Proprietăți la proiecția centrală:

1 este o proiecție a unui punct de punct.

2 Proiecția liniei este o linie.

3 Proiectarea unei linii drepte este, în general o linie dreaptă. (Dacă linia coincide cu fasciculul de proiecție, proiecția sa este punctul).

4 Dacă punctul aparține liniei, proiecția punctului aparține liniei de proiecție.

5 linii de la punctul de intersecție este proiectată la punctul de intersecție al proeminențelor acestor linii.

6 poliedru general plat proiectat poliedru cu același număr de noduri.

Proiecția 7 linii paralele între ele este un creion de linii.

8 Dacă o figură plană este paralelă cu planul de proiecție, proiecția sa este similară cu figura.

proiecție paralelă poate fi privit ca un caz special de proiecție centrale.

În cazul în care centrul proiecției la sediul central al proiecției să fie mutat la infinit, apoi proiectarea razele pot fi considerate paralele. Prin urmare, aparatul este alcătuit dintr-un plan de proiecție paralelă a direcțiilor de proiecție P și R. Când grinzile centrale de proiecție proeminente emerge dintr-un singur punct, și proiectarea paralelă - paralela.

În funcție de direcția de proiecție proiecție fascicul paralel poate fi oblică. atunci când se proiectează grinzi înclinate față de planul de proiecție și dreptunghiulare (ortogonale). atunci când razele proeminente sunt perpendiculare pe planul de proiecție.

Construirea unui segment paralel proiecție a1b1 AB pe planul P1 la o direcție predeterminată de proiecție P este P1. Acest lucru necesită proiecție linii drepte prin punctele A și B, în paralel cu proiecția P. La trecerea proiectându direct din P1 plan se obțin proiecții paralele A1 și punctele B1 A și B sunt conectate în proiecția paralelă a A1 și B1, obținem proiecția paralelă a segmentului a1b1 AB.

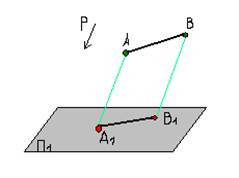
In mod similar, se poate construi o proiecție paralelă A1V1S1D1 patrulater ABCD pe planul P1 la o direcție predeterminată de proiecție P este P1.

Acest lucru necesită proiecție linii prin punctele A, B, C, D, paralelă cu R. direcția Când se obțin proiecția proeminentă liniilor de trecere cu proiecțiile plane P1 paralele A1, B1, C1, D1 punctele A, B, C, D. Combinarea proiecțiilor paralele A1, B1, C1, D1 obținem proiecția paralelă A1V1S1D1 ABCD patrulater.

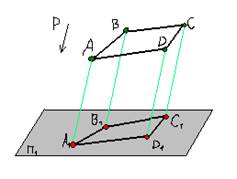
Proprietățile proiecțiilor proeminente în paralel:

1.Proektsii linii paralele paralele.

Se poate observa că liniile AA1, BB1, CC1 și DD1 formează două planuri paralele a și b. Aceste două planuri se intersectează cu P1. În consecință, linia de intersecție a a1b1 și S1D1 sunt paralele.

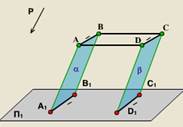
2. Dacă punctul împarte lungimea segmentului în ceea ce privește m: n, atunci proiecția acestui punct împarte lungimea proiecției segmentului pe aceeași bază.

Să punctul C aparține segmentului AB, și | AC |. | CB | = 1. 2. Să construim o proiecție paralelă a segmentului a1b1 AB. Punctul C1 a1b1. Desenați || AC“ A1C1 și CB „|| C1B1, vom obține două triunghiuri similare ACC „și CBB“. Asemănării lor ar trebui să fie proporțională cu părțile: | AC |. | CB | = | AC „|. | CB '|, dar | CB' | = | S1V1 | și | AC „| = | A1C1 |, deci | AC |. | CB | = | A1C1 |. | C1B1 |.

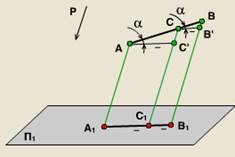
3. plat formă paralelă cu planul de proiecție este proiectată fără distorsiuni.

Ia triunghiul ABC și a proiecta pe două planuri paralele ale proiecțiilor P1 și P1. Deoarece segmentele de lungime egală cu | A1 A1 „| = | B1 B1 „| = | C1 C1 „| iar segmentele sunt paralele, patrulatere A1 A1 B1, B1 ', B1, B1 'S1S1', C1 S1'A1A1 „sunt paralelograme. În consecință, laturile opuse de lungime egală | A1 B1 | = | A1 'B1' |, | B1, C1 | = | B1 'C1' |, | A1 C1 | = | A1 „C1“ |, ceea ce înseamnă că triunghiuri sunt egale.

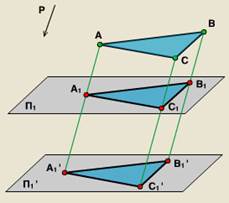
În mod similar, același lucru poate fi dovedit pentru orice alte forme plate. proiecție în paralel, spre deosebire de centrale posedă mai puțină claritate, dar oferă o mare simplitate de construcție și relația a originalului.

Așa cum am menționat mai sus proiecția ortogonală - un caz special de proiecție paralelă. În proiecție ortogonală raze proeminente sunt perpendiculare pe planul de proiecție.

Aparatul proiecției constă într-un singur plan de proiecție.

Pentru a obține proiecția ortogonală a punctului A prin este necesar să dețină fasciculul proeminente perpendicular pe P1. punctul A1 se numește proiecție ortogonală sau dreptunghiulare de la punctul A.

Pentru a obține proiecția ortogonală a segmentului a1b1 AB pe planul P1, este necesar, prin punctele A și B să dețină proiectarea liniilor drepte P1. La trecerea liniilor proeminente sunt obținute cu un plan P1 proiecții ortogonale A1 și B1 punctele A și B. Prin combinarea proiecții ortogonale A1 și B1 obține ortogonale segment de proiecție a1b1 AB.

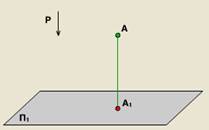
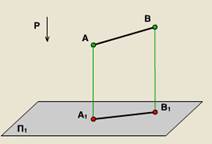
Toate proprietățile de proiecție proiecție fezabilă și ortogonale paralel. Cu toate acestea, proiecții ortogonale au unele mai multe proprietăți.

Proprietățile proiecția ortogonală:

Lungimea 1.Dlina egală cu lungimea proiecției sale împărțită la cosinusul unghiului de înclinare a segmentului la planul de proiecție.

Ia linia AB și să construiască proiecția ortogonală pe planul a1b1 P1. Dacă trage o linie dreaptă AS || A1b1, atunci triunghiul ABC, rezultă că | AC |. | AB | = Cos a și | AB | = | A1b1 |. cos o, t la | .. a1b1 | = | AC |.

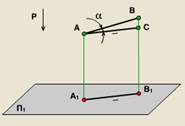
2. În plus, pentru teorema de proiecție ortogonală este despre proiectarea unghi drept:

Teorema: În cazul în care cel puțin o latură a unghiului drept este paralelă cu planul de proiecție, iar al doilea nu este perpendiculară, unghiul la acest plan este proiectat în mărime completă.

Dovada: Dan unghi drept ABC, care, prin ipoteză, linia BC AB si BC || P1 plan de proiecție. Prin construirea unei linii directe a soarelui este proiectat pentru a BB1. Ca urmare, soare direct la planul b (AVhVV1) t. K. la două linii intersectate. situată în planul. Prin condiția B1C1 directe || Soarele, astfel încât, de asemenea, la planul B, adică. E., și o a1b1 linie dreaptă acel plan. De aceea, unghiul dintre liniile drepte și B1C1 a1b1 este de 90 °, după cum este necesar.

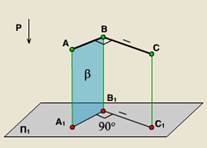
proiecție ortogonală construcții geometrice oferă ușurința în determinarea proiecțiile ortogonale ale punctelor, precum și capacitatea de a stoca pe proiecțiile formei și dimensiunilor figurii proiectate. Aceste avantaje au furnizat o proiecție ortogonală utilizată pe scară largă în desenul tehnic.

Metodele de proiecție de mai sus pot rezolva problema directă a geometriei descriptive, t. E. După construirea original, un desen plat. Proiecțiile astfel obținute pe un singur plan oferă o imagine incompletă a obiectului, forma și poziția acesteia în spațiul respectiv, adică. E. Nici un astfel de desen are proprietatea de reversibilitate.

Pentru a obține un desen reversibil, adică, desen oferind o imagine completă a forma, mărimea și poziția originalului în spațiu, desen odnokartinny complementului. În funcție de adăugările, există diverse tipuri de desene.

1.Epyur Monge sau proiecție ortogonală.

Metoda ortogonale (dreptunghiular) proeminenței este că originalul ortogonal proiectat pe două sau trei plane reciproc perpendiculare de proiecție și apoi să le combine cu planul desenului.

Esența axonometrică desen că prima originalul este asociat rigid cu un Oxyz sistem de coordonate cartezian, ortogonal proiectarea pe unul dintre avioanele sale de proiecție OXY sau OXZ. Apoi, proiecția paralelă sunt paralele cu proiecția Constructul rezultat: axele OX, OY, OZ, proeminențelor secundare și originalul.

În construirea perspectivă clădire desen prima o proeminență ortogonală, și apoi pe planul proiecției centrale sunt construite anterior și proiecția ortogonală a originalului.

4.Proektsii cu marcaje numerice etc ..

Pentru a obține proiecție cu marcaje numerice sunt proiectate ortogonal pe planul inițial de nivel zero și punctul de departe de punctul inițial pe planul.