Formula produs de sine, cosinus și sinus și cosinus

Studiul formulele de bază ale formulelor trigonometrice sinus continuă muncă, cosinus și cosinus sine. Aceste formule sunt, într-un sens invers formulele sume de sinus și cosinus. că este, să permită produsul de sinus și cosinus, și du-te la suma sau diferența de sinus și cosinus și.

În acest articol, considerăm următoarea formulă: produsul de sinus, cosinus ale produsului și produsul de sinus și cosinus, arată concluzia lor, și să dea exemple de utilizare a acestora.

Navigare în pagină.

lista cu formulele

Scriem ordinul cu formula produsului sinus, cosinus și cosinus sine.

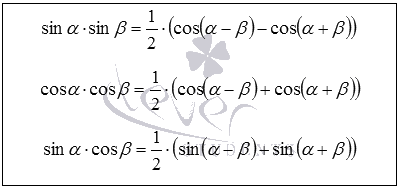
Aceste formule sunt valabile pentru orice unghiuri și.

Datele au exprimat produs formulare cu formula:

• Produsul din sinus unghiurilor și încă o jumătate de cosinusul unghiului și cosinusul unghiului.
• Produsul de cosinusului și egală cu jumătate din suma cosinusul diferenței unghiului și cosinusul și suma acestor unghiuri.
• Produsul sinusului și cosinusul unghiului unghiului este egal cu jumătate din suma și diferența dintre unghiurile sinusul și sinusul suma acestor unghiuri.

Derivarea cu formulele

Formula Product sinus, cosinus și sinus și cosinus pot fi derivate pe baza formulelor de adiție. precum și următoarea proprietate egalitati. în cazul în care partea stângă și dreaptă a ecuației corecte pentru a adăuga stânga și la dreapta, respectiv, a unei alte egalitate adevărată, obținem adevărata egalitate.

Pentru a obține formule produs de sinus și cosinus avem nevoie de suma cosinusul formulei și cosinus tipul și diferența.

Adăugarea acestor egalitati, obținem din care rezultă că. Astfel, sa dovedit a fi produs cu formula cosinusului.

Dacă suma formulei cosinus rescrie apoi pentru a adăuga această egalitate egalitate, apoi a obținut cu ușurință formă sinusoidală formula produsului.

Pentru derivarea sine și produsul cosinus suficient să se plieze laturile din stânga și dreapta cu formulele sum sinus și diferență sine. Avem, din care rezultă că.

Așa că am adus cu formula produsului de sinus, cosinus și sinus și cosinus.

exemple de utilizare

Să examinăm câteva exemple de produse formule de sinus, cosinus și cosinus sine. Acest lucru se face în scopul de a face clar ca sunt folosite mai vizualizate formule pentru unghiuri specifice.

Pentru a începe cu, verificarea validității, de exemplu, produsul formule sinusuri. Pentru aceasta vom lua, și verificați dacă aceleași valori ale pereților laterali dreapta și stânga ale acestor unghiuri. Avem (dacă este necesar, se referă la un tabel de valori ale sinus, cosinus, tangentă și cotangentă) și

Din moment ce avem aceeași valoare, produsul cu formula sine este valabilă pentru unghiurile.

În unele cazuri, cu formula produsului posibil să se calculeze valorile expresii trigonometrice. Să considerăm un exemplu care confirmă cuvintele noastre.

Se calculează valoarea exactă a produsului de sinus și cosinus de 75 de grade la 15 grade.

Valorile exacte sunt necunoscute pentru noi, deci nu putem calcula direct valoarea necesară. Cu toate acestea, răspunsul la întrebarea problemei ne permite să formula produsului de sinus și cosinus. Într-adevăr, suma unghiurilor 75 și 15 grade este de 90 de grade, iar diferența dintre ele este de 60 de grade, pentru că știm unghiurile exacte ale valorilor de date ale funcțiilor trigonometrice.

.

Funcții formula produsului sinus, cosinus, sinus și cosinus sunt folosite pentru a converti expresii trigonometrice. dar această problemă necesită o discuție mai detaliată.