Ecuația tangentei și ecuația normală a graficului

Tangent - este directă. care se referă la graficul funcției la un moment dat și toate punctele care sunt cel mai aproape de graficul funcției. Prin urmare, tangenta ruleaza pe graficul unui anumit unghi și nu poate trece prin punctul de tangență al tangentele mai multe unghiuri diferite. Ecuațiile tangentă și ecuații normale la graficul compilată folosind derivatul.

Ecuația tangentei este derivată din ecuația liniei.

Deducem ecuația tangenta, și apoi - ecuația normală la graficul funcției.

Să ne amintim ecuația unei linii cu panta:

În ea k - panta.

Prin urmare, obținem următoarea intrare:

Valoarea derivatei f „(x 0) a funcției y = f (x) la x 0 este egal cu panta k = tangent tgφ graficului trasată prin punctul M 0 (x y 0. 0). 0 unde y = f (x 0). Acesta este sensul geometric al derivatului.

Astfel, putem înlocui k prin f „(x 0) și se obține următoarea ecuație a tangentei la graficul funcției:

Sarcinile pentru prepararea ecuației tangentei la graficul funcției (și vom trece în curând pe ele) este necesară pentru a aduce formula dată mai sus pentru ecuația rezultată la o linie dreaptă într-un mod general. Pentru a face acest lucru, toate literele și numerele care urmează să fie mutat în partea stângă a ecuației, și dreptul de zero din stânga.

Acum, despre ecuația normală. Normal - aceasta este o linie dreaptă care trece prin punctul de contact perpendicular pe graficul tangenta. Ecuația normală:

Ne întoarcem la exemplele. Pentru soluții necesită un tabel de derivați (se deschide într-o fereastră nouă).

Exemplul 1. Crearea ecuație a tangentei și ecuația normală la graficul funcției în cazul în care abscisa punctului de tangență.

Decizie. Găsiți punct de contact ordonata:

Să ne găsim derivata funcției:

Găsim valoarea derivatului de la punctul de contact, adică raportul în unghi tangent:

Acum avem tot ceea ce este necesar pentru a înlocui în intrarea certificatului teoretic de mai sus pentru a obține ecuația tangenta. obține

În acest exemplu, am avut noroc: panta sa dovedit a fi zero, deci ecuația este condusă separat la aspectul general nu este necesară. Acum putem face ecuația normală:

Mai jos: program funcția visiniu tangentă verde, portocaliu normal.

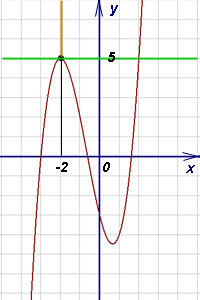
Următorul exemplu - nu este dificil: funcția, ca și în trecut, de asemenea, un polinom, dar coeficientul unghiular nu va fi zero, deci adăugați un pas - pentru a aduce ecuatia la forma generală.

Exemplul 2. Crearea ecuație a tangentei și ecuația normală la graficul funcției în cazul în care abscisa punctului de tangență.

Decizie. Găsiți punct de contact ordonata:

Să ne găsim derivata funcției:

Găsim valoarea derivatului de la punctul de contact, adică raportul în unghi tangent:

Substitut toate datele din „formulă-disc“ și obține ecuația tangentei:

Ecuațiile de vedere generală (toate cifrele și literele altele decât zero, se colectează pe partea stângă, iar rezerva dreapta la zero):

Echivaleaza la normal:

Exemplul 3. Creați ecuația tangentei și ecuația normală la graficul funcției în cazul în care abscisa punctului de tangență.

Decizie. Găsiți punct de contact ordonata:

Să ne găsim derivata funcției:

Găsim valoarea derivatului de la punctul de contact, adică raportul în unghi tangent:

Noi găsim ecuația unei tangenta:

Înainte de a reduce ecuația la o minte comună nevoie de ea un pic „perie“: multiplica pe termen de termen de 4. Făcând acest lucru duce la ecuația de forma generală:

Echivaleaza la normal:

Exemplul 4. Crearea ecuație a tangentei și ecuația normală la graficul funcției în cazul în care abscisa punctului de tangență.

Decizie. Găsiți punct de contact ordonata:

Să ne găsim derivata funcției:

Găsim valoarea derivatului de la punctul de contact, adică raportul în unghi tangent:

Noi obținem ecuația tangentei:

Aici este ecuația la forma generală:

Echivaleaza la normal:

O greșeală des întâlnită în prepararea ecuațiile tangentă și normală - nu a văzut că funcția, în acest exemplu - un complex și calcula derivatul său ca derivat al funcțiilor simple. Următoarele exemple - deja cu funcții complexe (lecție corespunzătoare se deschide într-o fereastră nouă).

Exemplul 5. Crearea ecuație a tangentei și ecuația normală la graficul funcției în cazul în care abscisa punctului de tangență.

Decizie. Găsiți punct de contact ordonata:

Atenție! Această caracteristică - un complex, din moment ce argumentul tangenta (2x) este ea însăși o funcție. Prin urmare, vom găsi derivata unei funcții ca un derivat al unei funcții compozit:

Găsim valoarea derivatului de la punctul de contact, adică raportul în unghi tangent:

Noi obținem ecuația tangentei:

Aici este ecuația la forma generală:

Echivaleaza la normal:

Exemplul 6. Crearea ecuație a tangentei și ecuația normală la graficul funcției în cazul în care abscisa punctului de tangență.

Decizie. Găsiți punct de contact ordonata:

Ca și în exemplul anterior, această funcție - este complicată, deoarece gradul de () este ea însăși o funcție. Prin urmare, vom găsi derivata unei funcții ca un derivat al unei funcții compozit:

Găsim valoarea derivatului de la punctul de contact, adică raportul în unghi tangent:

Noi obținem ecuația tangentei:

Aici este ecuația la forma generală:

Echivaleaza la normal: