Distanța dintre platforma de conținut de două linii drepte

Distanța dintre cele două linii drepte.

Regulată AVSA1V1S1 prisme triunghiulare,
toate marginile sunt egale cu 1, găsiți distanța dintre liniile AB și CB 1

Distanța dintre liniile oblice este distanța dintre una dintre liniile oblice și un plan care trece prin cealaltă paralelă cu prima linie.

Pentru a găsi distanța între două linii drepte care traversează, trebuie să:

• 1. După una dintre liniile de a ține planul paralel cu a doua linie.

• 2. Din orice punct al primei picături direct perpendicular pe planul și de a găsi lungimea sa. Adică, problema se reduce la a găsi distanța de la un punct la un plan.

Acest lucru se poate face printr-o geometrică sau prin metoda de coordonate.

Metoda geometrică Soluție

Direct a1b1 paralel cu linia AB. Prin a1b1 directe și B1C A1V1S plan paralel cu linia AB:

Ia-un punct M este punctul de mijloc al segmentului AB. Prin acest punct al MCC1 plan.

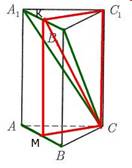
Arătăm că planul este perpendicular pe linia AB MCC1, și, prin urmare, A1V1S plan:

segmentul SM este mediana, și, prin urmare, înălțimea triunghiului echilateral ABC. KM directe CC1 drepte paralele și, prin urmare, perpendicular pe AB. Aceasta este linia dreaptă AB este perpendicular pe două linii care se intersectează MCC1 plan. și deci perpendicular pe planul.

Acum, ia în considerare în planul triunghiului dreptunghiular ISS MCC1 și țineți-l în înălțimea MR:

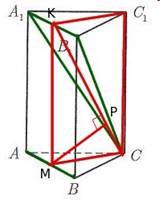
înălțimea LL lungimea triunghiului este distanța dintre liniile AB și CB 1, pe care trebuie să le găsim.

Pentru a găsi înălțimea MR, ne exprimăm ISS de două ori zona de triunghi

Metoda analitică pentru rezolvarea problemei:

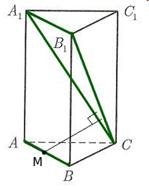
După cum ne amintim de metoda geometrică pentru rezolvarea acestei probleme, distanța dintre liniile AB și B1C este distanța de la punctul M, care este punctul de mijloc al segmentului AB la A1V1S avionul:

Distanța # 961; din punctul M0 (x0, y0, z0) la ploskostiax + de + cz + d = 0 se calculează cu următoarea formulă:

Punem prismă noastră a unui sistem de coordonate. Dacă vom rezolva problema cu un cub sau un paralelipiped dreptunghic, alegerea sistemului de coordonate este clar: am pus originea la unul dintre vârfurile cubului, și axa ghidajului de-a lungul marginilor. În cazul prismei nu este atât de evident.

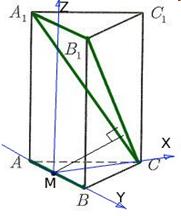
Ar trebui să aleagă un sistem de coordonate astfel încât coordonatele punctului M și punctele A1, B1 și C, definind un plan A1V1S calculat modul cel mai simplu și conținut cât mai multe zerouri posibil. Prin urmare, este convenabil de a alege un sistem de coordonate astfel:

• Notați coordonatele punctelor de care avem nevoie:

Pentru a găsi coeficienții a. b, c și d în ecuația ax + de + cz + d = 0 A1B1C plan take factor d = 1, și substituind coordonatele punctelor A1, B1 și C în ecuația plan. Un sistem de ecuații:

Substituind valorile coeficienților și coordonatele punctului M (0, 0, 0) în formula distanței.