Cum de a găsi o arie a secțiunii transversale diagonală

Diagonala secțiunii cub are forma unui dreptunghi, a cărui suprafață (S) este ușor de calculat, cunoscând lungimea fiecărei nervuri (a) o formă în vrac. Acest dreptunghi de una dintre părți ar fi înălțimea, care coincide cu o lungime de margine. Lungimea celeilalte - diagonale - mașinei de teorema lui Pitagora pentru triunghi, în care este ipotenuza și cele două margini ale bazei - picioarele. În termeni generali, acesta poate fi scris ca: * un √2. Aria secțiunii diagonale localiza înmulțirea a două laturi, a căror lungime ați găsit: S = a * o * = √2 a² * √2. De exemplu, atunci când lungimea muchiei de 20 cm aria secțiunii diagonale a cubului trebuie sa fie de aproximativ 20² * √2 ≈ 565686 cm².

Pentru a calcula aria secțiunii transversale a diagonalei paralelipipedului (S) procedează în același mod, dar rețineți că în teorema lui Pitagora în acest caz a implicat picioarele de diferite lungimi - lungimea (l) și cifrele lățime (w) de volum. Lungimea diagonalei în acest caz, va fi egală cu √ (l² + w²). Înălțimea (h), poate diferi de lungimile marginilor bazelor, astfel încât, în formula generală aria secțiunii transversale poate fi scrisă astfel: S = h * √ (l² + w²). De exemplu, în cazul în care lungimea, înălțimea și lățimea paralelipipedului sunt, respectiv, 10, 20 și 30 cm, aria secțiunii diagonală este de aproximativ 30 * √ (10² + 20²) = 30 * √500 ≈ 670,82 cm².

Diagonala piramida secțiune patrulateră are o formă triunghiulară. Dacă înălțimea (H) a poliedrului este cunoscută, iar la baza sa se afla un dreptunghi, lungimea muchiilor adiacente (a și b), care sunt, în aceleași condiții, calculul zonei (S) secțiunii transversale începe cu calcularea lungimii diagonalei bazei. Ca și în etapele anterioare de utilizare a celor două margini ale triunghiului și baza diagonală unde lungimea pitagoreică ipotenuzei este egal cu √ (a² + b²). Înălțimea piramidelor într-un poliedru coincide cu înălțimea triunghiului secțiunii diagonale. a redus la o parte, lungimea pe care tocmai ați definit. Prin urmare, pentru a găsi zona unui triunghi obține jumătate înălțimea produsului pe lungimea diagonalei: S = ½ * H * √ (a² + b²). De exemplu, la o înălțime de 30 cm, iar lungimile laturilor adiacente din suprafața secțiunii 40 și 50 cm diagonală de bază ar trebui să fie aproximativ egală cu ½ * 30 * √ (40² + 50²) = 15 * √4100 ≈ 960,47 cm².

Se calculează lungimea necesară. Folosind formula generală: lungimea muchiei piramidă sumă egală rădăcinii pătrate a diferențelor de coordonatele corespunzătoare ale punctelor de delimitare. Numerele de substituție coordonatele dvs. în formula și găsi lungimea marginilor piramidei. obține, de asemenea, lungimea coastelor nu numai piramidale regulate. dar dreptunghiulară și trunchiate, și arbitrar.

Găsiți lungimea coastelor piramidei. ale cărui margini sunt egale, cifrele stabilite partea de bază și înălțimea cunoscută. Determinați înălțimea locației unei baze, adică, punctul său mai mic. Deoarece coastele sunt egale, deci este posibil să se tragă într-un cerc, care este punctul de intersecție al diagonalelor centrul bazei.

Trasati o linie dreaptă care leagă colțurile opuse ale bazei piramidei. Marcați punctul în care se intersectează. Același punct și va fi o limită inferioară a înălțimii piramidei.

Găsiți lungimea diagonalei dreptunghiului folosind teorema lui Pitagora, în cazul în care suma pătratelor picioarele unui triunghi dreptunghic este egală cu pătratul ipotenuzei. Ia a2 + b2 = c2, unde a și b - picioare, și cu - ipotenuza. Apoi ipotenuzei este egală cu rădăcina pătrată a sumei pătratelor celorlalte două laturi.

Găsiți lungimea coastelor piramidei. În primul rând, împărțiți lungimea jumătate diagonală. Toate valorile de date recepționate pentru a substitui în formula pitagoreic descrisă mai sus. În mod similar cu exemplul anterior obține rădăcina sumei pătratelor înălțimea și jumătate din diagonala piramidei.

• Cum de a găsi lungimea laturii coordonatele

Se numește secțiune axială care trece prin axa geometrică a corpului format prin rotirea unei anumite figură geometrică. Cilindrul obținut prin rotirea în jurul uneia dintre laturile dreptunghiului, iar acestea se datorează proprietăților sale de multe. Formarea acestui corp geometric sunt paralele și egale între ele, ceea ce este foarte important să se determine parametrii secțiunii sale axiale, inclusiv pe diagonală.

• - cilindru cu parametri prestabiliți;
• - hârtie;
• - creion;
• - line;
• - busolelor;
• - teorema lui Pitagora;
• - Teorema de sinus și cosinus.

Construi cilindru în funcție de condițiile predeterminate. Pentru ca aceasta să atragă, trebuie să știți raza bazei și înălțimea. Cu toate acestea, alte condiții pot fi specificate în definiția sarcinii în diagonală - de exemplu, unghiul dintre diagonală și generatoarea sau baza diametrului. În acest caz, atunci când creați un desen folosind dimensiunea pe care ați setat. Restul ia un arbitrar și indică faptul că acesta este dat la tine. Desemnați punctul axa intersecție și baze O și O“.

Desenați secțiune axială. Este un dreptunghi, dintre care două laturi sunt diametrele bazelor și celelalte două - generatoare. Deoarece atât motivele perpendiculare care formează acestea sunt ambele înălțimi ale corpului geometric. Desemnați dreptunghiului rezultat ca ABCD. Cheltuiți AC diagonală și BD. Amintiți-vă proprietățile diagonalele dreptunghiului. Ele sunt egale între ele și împărțită în jumătate, la punctul de intersecție.

Luați în considerare triunghiul ADC. Are dreptate, pentru că CD-imagine este perpendiculară pe sol. Un picior este un diametru al bazei, al doilea - formare. Diagonala este ipotenuza. Gândiți-vă cum să calculeze lungimea oricărei ipotenuzei unui triunghi dreptunghic. Acesta este egal cu rădăcina pătrată a sumei pătratelor celorlalte două laturi. Aceasta este, în acest caz, d = √4r2 + h2, unde d - diagonală, r - raza bazei, și h - înălțimea cilindrului.

Dacă problema nu este dat înălțimea cilindrului, dar unghiul specificat secțiune axială pe diagonală cu o bază sau prin utilizarea sinus sau cosinus teorema. Să ne amintim că media funcțiile trigonometrice de date. Este o relație de opusul sau contigue predeterminat unghiul piciorului la ipotenuzei, că tu și să fie găsit. Să presupunem că setați înălțimea și unghiul dintre CAD si diagonala a diametrului de bază. În acest caz, utilizați legea Sines, deoarece unghiul CAD este generatoarei opusă. Localizați ipotenuza d cu formula d = h / sinCAD. Dacă setați raza și același unghi, utilizați teorema lui cosinus. În acest caz, d = 2r / cos CAD.

Prin același principiu se aplică în cazurile în care se specifică unghiul ACD între diagonală și generatorul. În acest caz, teorema sine este utilizat atunci când o rază și cosinus dat - dacă știi cota.

Construire a unei linii de intersecție cu suprafață plan frontal-proeminente piramida Σ (Σ2).
În primul rând marca punctele dorite de secțiuni care pot fi determinate fără avioane secțiuni auxiliare.

Σ intersectează planul de bază al piramidei în linie dreaptă 1-2. Notă punctul 12≡22 - vedere frontală a acestei linii drepte - și prin intermediul unei legături verticale construi proiecțiile lor orizontale 11,21 pe părțile laterale și A1C1 bază B1C1

Rib SA (S2A2) intersectează planul piramidei sigma (Σ2) la punctul 4 (42). Proiecția orizontală folosind coaste S1A1 obține punctul de link-ul 41.

3 prin punctul (32) execută ca un plan de tăiere auxiliar nivel plan orizontal T (T2). Acesta este paralelă cu planul de proiecție P1 și într-o secțiune cu o suprafață a piramidei voinței triunghiului similar cu baza piramidei. La S1A1 E1 marchează punctul în S1S1 - punctul K1. Desenați linii paralele cu laturile A1V1S1 baza piramidei, și a obține S1V1 punct de margine 31. unește punctele 11, 21, 41, 31, primi proiecția orizontală a planului predeterminat dorit piramidal suprafață secțiune. secțiunea frontală de proiecție coincide cu proiecția frontală plană sigma (Σ2).

La S1A1 E1 marchează punctul în S1S1 - punctul K1. Desenați linii paralele cu laturile A1V1S1 baza piramidei, și a obține S1V1 punct de margine 31. unește punctele 11, 21, 41, 31, primi proiecția orizontală a planului predeterminat dorit piramidal suprafață secțiune. secțiunea frontală de proiecție coincide cu proiecția frontală plană sigma (Σ2).

Astfel, problema este rezolvată, reieșind din principiul găsit de puncte care aparțin simultan două elemente geometrice - suprafața de piramidă și un plan de tăiere predeterminat Σ (Σ2).

Încercați o problemă mai generală pentru a analiza în detaliu construcția secțiunii transversale a cubului.
Lăsați linia de intersecție planul de tăiere definit propriul său plan și planul care conține baza de jos a casetei l și unghiul la planul p.
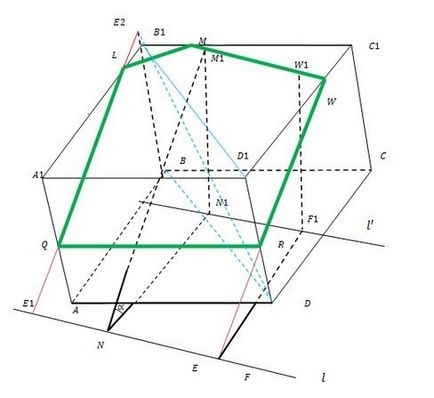
Întregul principiu de construcție este ilustrat în figura.

Decizie.
Orice unghi de probleme geometrice privind construcția nu este specificată de unghiul, și oricare dintre funcției sale trigonometrice, lăsați-l să fie cotangentă (CTG). Este necesar să se măsoare în orice soluție sistem Compas lungime metric Nctgf = d. Mutați această valoare în amploarea problemei și, bazată pe principiul similitudinii triunghiurile cu un unghi ascuțit comun, efectuați următoarele.

L pe linia ia două puncte arbitrare N și F (deci este de dorit ca toate să fie continuată în continuare în cadrul inferior bazei ABCD cub). Dintre acestea, ca centru, trage o rază arc d în ABCD. Aceste arce glisează comune tangent l până la intersecția cu AB și CD (poate continua). atingeți marca punctul N1 și F1.

De la N1 și F1 este necesar pentru a ridica perpendicularele M1 și W1 pe baza superioară A1B1C1D1, a cărei lungime este egală cu N. Prin urmare, punctul de intersecție să se uite nu este necesar, deși este destul de simplu. Acum extinde segmentul M1W1 pentru a suprima cu B1C1 și S1D1 în M și W, respectiv. Deci ai găsit prima parte a secțiunii dorite MW.

Apoi, în planul care conține lateral cu fața DCC1D1, trage o linie de la punctul WE W (E - intersecția cu linia dreaptă l). WE intersecția cu D1D - punctul R. Cut WR - a doua muchie a secțiunii dorite.

Extindeți marginea laterală BB1 a cubului în direcția de la B la B1. Avionul diagonal al liniei BB1D1D R swipe-cub secțiune până la intersecția cu o BB1 extensie la punctul E2. Din această linie de jos până la intersecția cu L E1. E1E2 directă intersectează marginile laterale ale cubului și a1b1 AA1 la punctele L și Q, respectiv. Apoi ML, LQ și QR - rămasă dorită secțiunea nervură a cubului.

În multe manuale au găsit locuri de muncă legate de construirea de secțiuni de diferite forme geometrice, inclusiv cutia. Pentru a face față cu o astfel de sarcină, acesta ar trebui să fie înarmat cu unele cunoștințe.