Cum de a găsi ecuația de tangenta la graficul

Tangenta la curba - o linie care este adiacentă acestei curbe, la punctul dat, adică se extinde prin aceasta, astfel încât o suprafață mică în jurul acestui punct este posibil fără prea multă pierdere de precizie pentru a înlocui segmentul curbei tangentei. Dacă această curbă este un grafic al funcției, tangenta la aceasta este posibil să se construiască o ecuație specială.

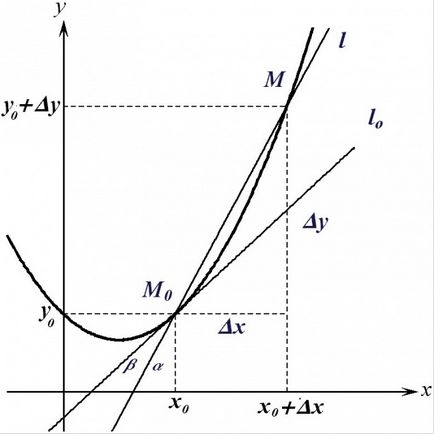
Să presupunem că aveți graficul unei funcții. Două puncte de pe această diagramă, puteți desena o linie dreaptă. O astfel de linie intersectează funcția dată grafic la două puncte numite secante.

În cazul în care, lăsând primul punct de pe teren, a muta treptat al doilea punct în direcția ei, secantă se va roti încet, tinzând spre o anumită poziție. În cele din urmă, atunci când cele două puncte de îmbinare într-una singură, divizat se va potrivi perfect în programul dumneavoastră în acest singur punct. Cu alte cuvinte, secantei rândul său, la Tangent.

Orice înclinat (adică, nu pe verticală) linie trasată pe planul de coordonate este graficul ecuației y = kx + b. Secant care trece prin punctele (x1, y1) și (x2, y2), astfel trebuie să respecte următoarele condiții:
KX1 + b = y1, KX2 + b = y2.
Rezolvarea acestui sistem de două ecuații liniare, obținem: KX2 - KX1 = y2 - y1. Astfel, k = (y2 - y1) / (x2 - x1).

Atunci când distanța dintre x1 și x2 la zero, diferența de diferențialele rândul său. Astfel, în ecuația tangentei se extinde prin punctul (x0, y0) Coeficientul k este egal ∂y0 / ∂x0 = f „(x0), adică valoarea derivatei funcției f (x) la x0.

Pentru a afla coeficientul b, substitui valoarea deja calculată k în ecuația f „(X0) * x0 + b = f (x0). Rezolvarea acestei ecuații în ceea ce privește b, descoperim că b = f (X0) - f „(X0) * x0.

Versiunea finală a ecuației tangentei la graficul funcției în punctul x0 dat, este după cum urmează:
y = f „(x0) * (x - x0) + f (x0).

Ca un exemplu, să considerăm ecuația tangentei funcției f (x) = x ^ 2, la un punct x0 = 3. Derivat de x ^ 2 este 2x. În consecință, ecuația tangentei devine:
y = 6 * (x - 3) + 9 = 6x - 9.
Valabilitatea acestei ecuații este ușor de verificat. Diagrama liniei y = 6x - 9 trece prin același punct (3; 9) și că parabole original. După ce a construit ambele grafice, puteți vedea că acest lucru este într-adevăr un contact direct cu parabolei în acest moment.

Astfel, graficul funcției are o tangentă la punctul x0 doar când funcția are un derivat de la acest punct. În cazul în care funcția punctul X0 are discontinuitate de al doilea tip, devine tangent la o asimptotă verticală. Cu toate acestea, simpla existență a derivatului într-un punct x0 nu garantează existența indispensabilă a tangentei la acest punct. De exemplu, funcția f (x) = | x | la punctul x0 = 0 este continuă și diferențiabilă, ci o tangentă la ea în acest moment este imposibil. Formula standard în acest caz dă ecuația y = 0, dar această linie nu este tangent la modulul grafic.

• Matematica pentru elevi - ecuația tangentei
• Scrieți ecuația tangentei

La elaborarea ecuația tangentei la graficul noțiunii de „abscisa punctului de contact.“ Această valoare poate fi stabilită inițial în condițiile problemei, sau trebuie să fie determinată în mod independent.

Egal foaie pentru o celulă de axele de coordonate x și y. Examinați ecuația dată pentru graficul funcției. Dacă este liniar, este suficient să se cunoască două valori pentru parametrul y pentru orice x, iar apoi a construi aceste puncte de pe axele de coordonate, și să le conectați printr-o linie dreaptă. Dacă graficul de un non-liniar, apoi face un tabel în dependență de x și ridica cel puțin cinci puncte pentru complot.

Se trasează funcția și setată la o axă predeterminată de coordonate a punctului de tangenta. În cazul în care coincide cu funcția, x coordonata este egală cu litera „a“, care este indicată de abscisa punctului de tangență.

Se determină valoarea punctului abscisa atingere pentru cazul în care punctul setat nu coincide cu graficul funcției tangentă. Selectați a treia opțiune este litera „o“.

Functia de ecuația f (a). Pentru a face acest lucru, ecuația originală pentru x și substitut. Găsiți derivata funcției f (x) și f (a). Substitut datele necesare în ecuația generală a tangentei, care are forma: y = f (a) + f „(a) (x - a). Ca rezultat, o ecuație care este format din trei parametri necunoscuți.

Pune-l în loc de coordonatele x și y ale unui punct dat, prin care tangenta. Apoi găsește soluția ecuației obținută pentru toți o. Dacă este pătrat, vor exista două valori ale punctului de abscisă atingere. Acest lucru înseamnă că tangenta este loc de două ori în apropierea graficul funcției.

Desenați un grafic al unei funcții date, și paralelă cu linia, care este, de asemenea, starea problemei. În acest caz, de asemenea setat ca parametru necunoscut și substitui-l în ecuația f (a). Echivala f derivat (a) derivata liniei paralele ecuației. Această acțiune vine de la starea de paralelism a celor două funcții. Găsiți rădăcinile ecuației rezultată, care va fi abscise punctul de tangență.

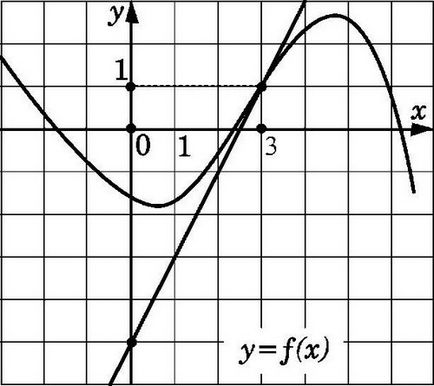
Direct y = f (x) este tangenta la graficul prezentat în figura la x0 în cazul în care acesta trece prin punctul (x0; f (x0)) și are un coeficient unghiular f „(x0). Găsiți un coeficient știind deosebit de completare snap tangentă.

• - carte de referință matematică;
• - un creion;
• - notebook-uri;
• - echer;
• - busolelor;
• - pen.

Rețineți că graficul unei funcții diferențiabile la x0 f (x) este aceeași ca și segmentul tangentei. Având în vedere acest lucru, este suficient de aproape de lungimea I, care trece prin punctul (x0; f (x0)) și (x0 + Ax; f (x0 + Ax)). Pentru a specifica o linie dreaptă, care trece printr-un anumit punct A cu coeficienți (x0; f (x0)), trebuie să indice panta. Coeficientul unghiular este Dy / tangentă secant Ax (bH → 0) și tinde la numărul f „(x0).

Dacă valorile f „(x0) nu există sau nu tangențial, sau se extinde vertical. Având în vedere acest lucru, existența derivatului funcției la x0 datorită existenței tangent non-vertical în contact cu funcția program la punctul (x0, f (x0)). În acest caz, coeficientul de colț este tangentă este f „(X0). Astfel, devine clar înțeles geometric al derivatului - calculul pantei tangentei.

Desenați figura tangentele suplimentare care ar veni în contact cu graficul functiei la punctele x1, x2 și x3 și verificați unghiurile formate de aceste tangente cu abscisa (unghiul este numărată într-o direcție pozitivă de la axa la linia tangentă). De exemplu, primul unghi, adică, α1, va fi ascuțit, al doilea (a2) - obtuz, iar al treilea (a3) ​​este zero, deoarece linia tangentă trasată paralel cu axa OX. În acest caz, unghiul obtuz tangenta - o valoare negativă, tangenta un unghi ascuțit - pozitiv, iar dacă rezultatul este zero tg0.

determina corect unghiul format de tangenta. Pentru a face acest lucru, utilizați un echer.

Două linii drepte sunt înclinate în paralel, dacă coeficienții unghiulare sunt egale între ele; perpendicular, dacă produsul coeficienților unghiulare ale tangenta este -1.

• Tangenta la graficul funcției

Înainte de a trece la determinarea coordonatelor punctului de atingere, verificați posibilitatea unei tangenta. Pentru aceasta, analiza funcției, care descrie o anumită curbă la un anumit site.

Linia tangentă la un plan arbitrar într-un sistem de coordonate rectangulare - este limita la care tinde secant la această curbă la cea mai apropiată abordare a punctelor de intersecție a curbei și linia dreaptă.

În consecință, tangenta are un singur punct comun de pe curba. Cu toate acestea, această afirmație este adevărată pentru o zonă bine definită. În funcție de comportamentul curbei în celelalte zone ale planului de coordonate, linia tangentă poate intersecta o versa predeterminată sau vice, departe de ea.

Unele curbe pot desena o tangentă în orice punct. Exemple de astfel de linii - cerc, elipsa. Alte curbe continue pot fi punctul la care este imposibil de a construi o tangentă. Aceasta are loc în zonele în care transversale nu aspiră la aceeași poziție limită.

Să presupunem că o curbă arbitrară este descrisă de expresia Y = F (x). Forma generală a ecuației drepte Y = kx + o. Evident, la punctul de tangență cu coordonatele (XO, YO) ecuația: F (Xo) = KXO + a.

Dacă funcția F (x) este diferențiabilă în punctul Xo, în acest moment se poate trage o tangentă la curba si panta tangentei la axa OX este valoarea funcției derivat: k = F „(Xo). Ecuația tangentei la punctul de contact devine Yo = F „(Xo) * Xo + a. Problema găsirii coordonatelor punctului de atingere se reduce la rezolvarea unui sistem de două ecuații cu două necunoscute Yo = F (Xo) și Yo = F „(Xo) * Xo + a.

Avionul este tangentă la suprafața dacă suprafața are un punct comun și o linie dreaptă sau curbă plană. Determinarea coordonatelor (Xo Yo Zo) punctul comun al planului tangent al suprafeței curbe și Z target = F (x, y) este posibilă în cazul în care funcția F (x, y) are un diferențial complet în acest punct.