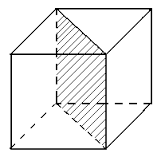
Cum de a găsi aria secțiunii diagonale a cubului

Aria secțiunii diagonale cub este foarte ușor de găsit dacă știi valoarea din coastele lui, sau zona de o fata.

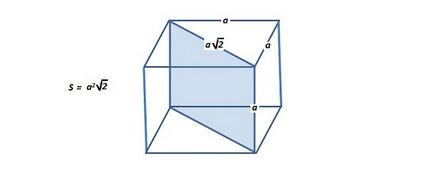
Dacă valoarea cunoscută a marginii cub, atunci suprafața secțiunii transversale a constatat prin formula

S (secțiunea diagonală) = 1.414 * o * o *

Dacă știți zona uneia dintre fețele cubului, atunci formula suprafeței cubică secțiune va arăta astfel

S (secțiunea diagonală) = 1,414 * S (fețe de cub)

Notă - pentru comoditate în loc de rădăcina a două scrise valoarea numerică rotunjită la cea mai apropiată miime.

moderatorul a ales cel mai bun răspuns

Axial secțiune transversală a cubului este un dreptunghi, din care o parte este egală cu lungimea nervurii, iar celălalt - se confruntă cu diagonală. Dacă muchia este cunoscută și egală cu o. Apoi, fațetele diagonală este atât ipotenuzei echilateral unui triunghi dreptunghic ale cărui picioare sunt - este de două margini adiacente ale unui cub sau două laturi ale feței pătrat. Prin urmare diagonală (ipotenuza) poate fi calculată prin teorema lui Pitagora, lungimea sau nervură și raportul la 45grad sinus (sau cosinus) (o jumatate dintr-un unghi drept). Sinus 45grad egală cu jumătate din pătrat. rădăcină de 2 sau 0.707. Prin urmare, diagonala b = a / 0,707. Și zona diagonalei unui pătrat secțiune transversală:

S = a * b = (a ^ 2) /0.707

(În cazul în care o ^ 2 - este un pătrat sau în al doilea grad).

Găsirea secțiunea diagonală pătrat a cubului nu este o sarcină complicată, deoarece cubul toate laturile sale sunt egale, iar fețele sunt pătrate. Prin urmare, dacă vă construi un cub-secțiune care trece prin fețele opuse pe diagonală, obținem un dreptunghi în care laturile mai mici par egal cu cubul, lăsați-l să fie una din laturile lungi clasic și va fi egală cu diagonala unui pătrat cu latura A.

Formula pentru a găsi aici diagonalele:

Suprafața unui dreptunghi - este produsul dintre laturile sale, și apoi formula pătratului secțiunii diagonale a cubului ia forma: