Coeficientul de corelație și de covarianță

Anterior a fost discutat diagramă de dispersie, ilustrând distribuția de date numerice bidimensionale (a se vedea. Ultima secțiune a reprezentării imaginii bidimensionale a datelor numerice note de date numerice în formă de tabele și diagrame). În această lucrare vom examina doi indicatori cantitativi care caracterizează raportul de putere dintre cele două variabile - covarianța și coeficientul de corelație. [1] Covarianța estimează din cauza relației liniare dintre două variabile numerice X și Y. Proba covarianță:

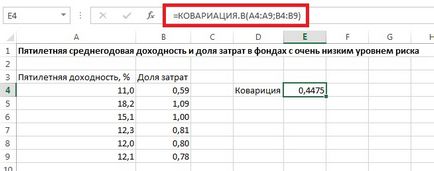
Fig. 1. Randamentul mediu de cinci ani, iar ponderea costurilor de fonduri mutuale cu risc foarte scăzut

Curios, covarianța variabilei aleatoare cu o variație egală cu:

În cazul în care covarianța este pozitiv, odată cu creșterea valorilor unei variabile aleatoare, a doua valoare tinde să crească, iar în cazul în care semnul este negativ - acea scădere. Cu toate acestea, numai valoarea absolută a covarianța este imposibil de a judeca cât de mult valoarea interconectate, deoarece aceasta depinde de amploarea dispersiei lor. Scala poate normaliza prin împărțirea la produsul valorii covarianței deviație standard (rădăcina pătrată a varianței). Acest lucru conduce la o așa-numitul coeficient de corelație Pearson.

În funcție de puterea relativă sau conexiunea, între cele două variabile care constituie eșantionul măsurat coeficientul de corelație bidimensional, care variază de la -1 la o proporție inversă ideală pentru una o proporție perfectă directă. Coeficientul de corelație este notată cu litera grecească care p. Liniaritatea corelației înseamnă că toate punctele indicate pe diagramă scatter, se află pe o linie dreaptă (Figura 2). Panoul A prezintă o dependență liniară între variabilele X și Y. Astfel, coeficientul de corelație este care p egal cu -1, adică, când variabila X crește, Y scade variabila. Panoul B prezintă o situație, în care între variabilele X și Y au corelația. În acest caz, coeficientul de corelație care p este egal cu 0, și atunci când variabila X crește, Y variabilă nu prezintă nici o tendință certă: ea nu scade nici nu crește. Panoul B prezintă o corelație directă între variabilele liniare X și Y. Astfel, coeficientul de corelație care p este egal cu 1, iar atunci când variabila X crește, Y variabilă crește de asemenea.

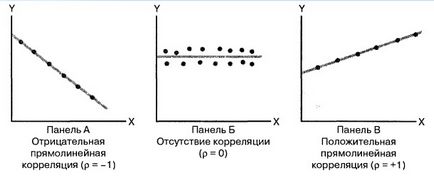
Fig. 2. Trei tipuri de relație între două variabile

La analiza probelor conținând un eșantion bidimensională coeficient de corelare a datelor calculat, care este notat cu r literă. În situații reale coeficientul de corelație ia rareori valori precise -1, 0 și +1. Fig. 3 prezintă șase diagrame scatter și coeficienții de corelație corespunzătoare r între variabila valori 100 X și Y.

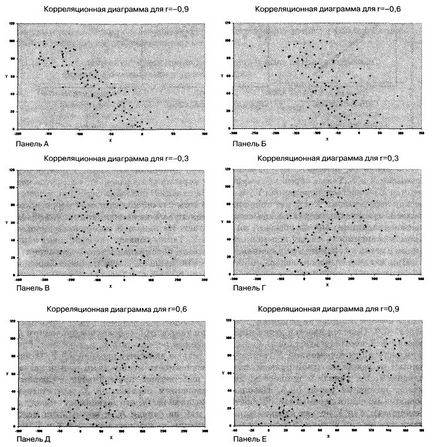
Fig. 3. Șase diagrame de dispersie și a coeficienților de corelație corespunzătoare obținute prin programul Excel

Panoul A prezintă situația în care proba coeficientul de corelație r este egal cu -0.9. A observat o tendință clară: valori mici ale lui X corespund valori foarte ridicate ale variabilei Y, și, invers, valori mari ale lui X corespund valorilor mici ale variabilei Y. Cu toate acestea, datele nu se află pe o linie dreaptă, astfel încât relația dintre ele nu pot fi numite liniare. Panoul B prezintă mostră de date coeficientul de corelație dintre ele este egal cu -0.6. Valorile mici ale X corespund valorilor mari ale variabilei Y. Rețineți că relația dintre variabilele X și Y nu pot fi numite liniare ca în panoul A, iar corelația dintre ele nu este atât de mare. Coeficientul de corelație dintre variabilele X și Y, reprezentată în panoul B, egal cu -0.3. A observat o ușoară tendință, potrivit căreia valori mari ale variabilei X, în general, corespund valorilor mici ale variabilei Y. Panels D-F ilustrează corelații pozitive între date - scăzute valori variabile X corespund valorilor mari ale variabilei Y.

Discutând Fig. 3, am folosit tendința pe termen, deoarece între variabilele X și Y nici o relație cauză-efect. Corelația nu implică relații cauzale între variabilele X și Y, adică, modificarea valorii unei variabile nu duce neapărat la o modificare a valorii unui alt. Corelarea puternică poate fi aleatoare și oa treia variabilă specială care rămâne în afara analizei. În astfel de situații, este necesar să se efectueze cercetări suplimentare. Astfel, se poate argumenta că relațiile cauzale generează corelație, dar corelația nu implică relații cauzale.

Coeficientul de corelație selectivă:

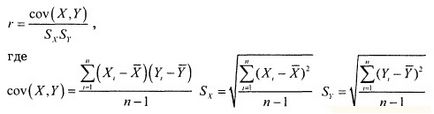
Deoarece funcția Excel CORREL utilizat = () (fig. 4) pentru calcularea coeficientului de corelație.

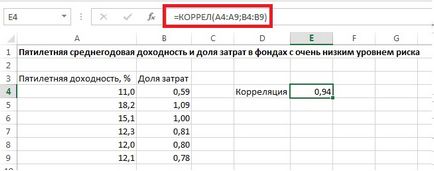
Fig. 4. Funcția CORREL în Excel

Astfel, coeficientul de corelație indică o relație liniară sau o conexiune între cele două variabile. Mai aproape coeficientul de corelație este de -1 sau +1, cu atât mai puternică relația liniară între două variabile. Semnul coeficientului de corelație determină natura relației: directă (+) și înapoi (-). O corelație puternică nu este o relație de cauzalitate. Acesta indică doar o caracteristică tendință a eșantionului.