Clasa de fizică și matematică

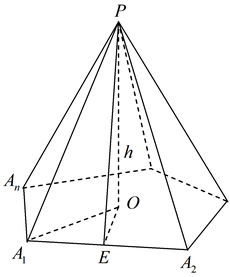
Piramida numit poliedru se confruntă cu una dintre care este un poligon arbitrar, iar cealaltă parte - triunghiuri cu un nod comun.

O perpendiculară trasată de la vârful piramidei la planul de bază, numit înălțimea piramidei.

Tetraedru - o piramidă a cărei bază este un triunghi.

Triunghiuri care alcătuiesc tetraedru, numit fețele sale. partea lor - coaste. iar partea de sus - partea de sus a tetraedrului. Două margini ale unui tetraedru care nu are noduri comune sunt numite opuse. De obicei, izolate de la una margini tetraedru și numit baza sa. iar celelalte fețe sunt numite fețe laterale.

tetraedru regulat este numit un tetraedru ale cărui toate marginile sunt egale.

În mod corespunzător numit această piramidă piramidă, în cazul în care baza sa - un poligon regulat, iar înălțimea de bază a piramidei coincide cu centrul poligonului. Linia care conține înălțimea corectă a piramidei se numește axa sa.

Înălțimea fața laterală a unei piramide regulate trase din partea superioară a acesteia, numit apotemă.

piramida trunchiată (vezi. continuare) este corectă. în cazul în care se obține o piramidă regulată secțiune plan paralel cu baza. Baza dreapta trunchiate piramida - poligoane regulate și fețele laterale - trapez isoscel. Înălțimea trapezoidal numită piramidă apotemă trunchiate.

Luați în considerare următoarele afirmații:

Marginile laterale ale piramidei sunt egale.

Marginile laterale ale piramidei sunt la fel de înclinate spre baza piramidei.

Partea superioară a piramidei este proiectată în centrul cercului circumscris despre baza piramidei.

Înălțimile fețele laterale ale piramidei, extrase din vârful piramidei, sunt egale, iar înălțimea piramidei se află în interiorul piramidei.

Toate unghiurile diedre de la baza piramidei sunt egale.

Partea superioară a piramidei este proiectată în centrul unui cerc înscris în baza piramidei.

Regulate piramidă triunghiulară opuse marginile pairwise perpendiculare.

Dacă marginile laterale ale piramidei sunt egale, atunci baza este un poligon regulat în jurul căruia poate fi descris printr-un cerc, iar vârful piramidei este proiectată în centrul acestui cerc.

Dacă unghiurile diedre de la baza piramidei sunt egale, atunci baza piramidei este un poligon, care poate fi înscris într-un cerc și un vârf al piramidei este proiectată în centrul acestui cerc.

Declarațiile 1, 2, 3, 4, 5, 6 sunt echivalente.

Secțiunea transversală a piramidei cu un plan paralel cu baza

Secțiunea transversală a piramidei cu un plan paralel cu baza (înălțime perpendicular) sa împarte înălțimea și marginile laterale ale piramidei în segmente proporționale.

Secțiunea transversală a piramidei cu un plan paralel cu baza (înălțime perpendicular) sa are o bază poligon asemănător piramidei, iar coeficientul de similitudine poligoanelor este egal cu raportul dintre distanțele lor de la vârful piramidei.

secțiuni transversale pătrate paralelă cu baza piramidei sunt pătrate de distanțele lor de la vârful piramidei.

Suprafața și volumul piramidei

Să presupunem că - înălțimea piramidei, - perimetrul bazei piramidei, - suprafața de bază a piramidei, - suprafața laterală a piramidei, - suprafața totală a piramidei, - volumul piramidei. Apoi, avem următoarele relații:

Dacă toate unghiurile diedre de la baza piramidei sunt egale, iar înălțimile toate fețele laterale ale piramidei, extrase din vârful piramidei, sunt egale,