Calcularea distanței dintre două linii și să coordoneze toate comune perpendiculare

Coordonează toate comune perpendicular pe două linii de trecere sau intersectate.

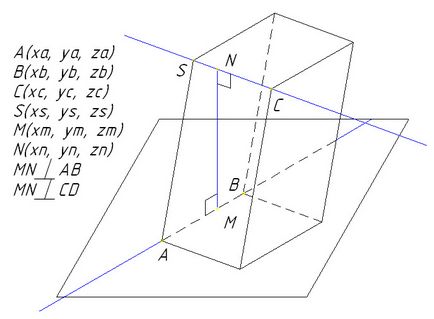
În spațiul dat la patru puncte:

Liniile AB și CS sunt de înclinare sau se suprapun.






Găsiți coordonatele tuturor comune perpendicular pe liniile AB și CS

Să cinci condiții:

1. Punctul M (xm, ym, zm) aparține unei linii drepte AB;
2. Punctul N (xn, yn, z6) aparține unei linii drepte CS;
3. MN direct perpendicular pe linia AB;
4. MN direct perpendicular pe linia CS;
5. Liniile AB și CS nu sunt paralele;

Apoi, segmentul [MN] este comun perpendicular pe liniile AB și CS. iar lungimea intervalului [MN] este cea mai scurtă distanță între liniile drepte AB și CS.

Efectuat următoarele cinci cinci condiții:

Coordonate (coliniare) vectori paralele sunt proporționale.

Produsul scalar al vectorilor perpendiculari (ortogonale) este zero.

Coliniare vectori produsul vectorial nu este egal cu vectorul zero. Modulul produsului vectorial al vectorilor non-coliniare strict mai mare decât zero.

Prin ipoteză, deoarece liniile AB și CS nu sunt paralele, produsul vectorial

, Următoarele cinci condiții:

Ne exprimăm xm din primele două ecuații. ym. zm. xn. YN. zn

Am găsit coordonatele MN vectorului

Substituind xm. ym. zm. xn. YN. zn în a treia și a patra ecuație, vom găsi m și n:

Obținem un sistem de două ecuații cu două necunoscute m. n.

Avem următorul sistem de două ecuații cu două necunoscute m. n:

Deoarece patratul produsului interior al vectorilor non-coliniare întotdeauna strict mai mică decât produsul dintre pătratelor modulii acestor vectori, determinant principal al acestui sistem:

Prin urmare, acest sistem are o soluție unică.

Coordonate toate comune perpendicular [MN] la cele două linii oblice. Segmentul [MN] este perpendicular AB și perpendicular SC

Coordonatele punctului M (xm, ym, zm). situată pe o linie AB:

Coordonatele punctului N (xn, yn,, Zn). situată pe linia SC.

Coordonează toate comune perpendicular oblic (sau crossover-ul) Direct AB și CS:

Distanța dintre liniile drepte neparalele.

Două modalități de calcul a distanței dintre liniile drepte neparalele.

Distanța dintre liniile neparalele drepte AB și CS pot fi găsite prin formula:

Distanța dintre linii drepte neparalele AB și SC poate fi găsit un al doilea mod, înălțimea bazei paralelipiped ale cărei laturi sunt [AB] și [SC]. și o nervură laterală este [AS].

Prin deplasarea punctului de pornire al vectorului în SC A. va construi o cutie de pe vectorii AB. SC. AS. al cărui volum este egal cu modulul produsului mixt vectorii AB. SC. AS. o suprafață de bază egală cu modulul produsului vectorial al vectorilor AB și SC. Distanța dintre liniile AB si SC egală cu înălțimea paralelipipedului construit pe vectorii AB. SC. AS.

produs Vector AB si SC are coordonatele:

produsul vectorial al vectorilor Modul AB și SC.

Modul AS vectori produs mixt. AB. SC:

Cea mai mică distanță dintre liniile AB și CS pot fi găsite de formula:

Distanța dintre liniile paralele AB și CS

Distanța dintre liniile paralele AB și CS este distanța de la punctul de S (xs, ys, zs) la linia AB.

De asemenea, există două modalități de a găsi distanța dintre două linii paralele, adică două moduri de a găsi distanța de la un punct la o linie. În primul rând, vom găsi coordonatele punctului de proiecție pe linie. AB directă este dat coordonatele a două dintre punctele sale

Punctul K este proiecția punctului S pe linia AB.

Găsiți coordonatele punctului K

Pentru a găsi coordonatele condițiilor de utilizare punctul K:

1. Vectori AK și AB - sunt coliniari, coordonatele lor sunt proporționale;
2. Vectori SK și AB sunt ortogonale, iar produsul lor scalar este zero;

Din prima ecuație

Substituind XK. yk. ZK în a doua ecuație, găsim T:

Coordonatele punctului de proiecție S pe linia AB. adică coordonatele punctului K (xk, yk, zk):

Distanța dintre punctul de S și o linie dreaptă AB poate fi găsit prin formula:

Distanța dintre punctul de S și o linie dreaptă AB poate fi găsit un al doilea mod, ca înălțimea unui paralelogram, laturile care sunt [AB] și [AS].

Produsul vectorial al vectorilor AB și AS are coordonatele:

produsul vectorial al vectorilor AB Modul și AS:

Amploarea AB:

Distanța dintre punctul de S și o linie dreaptă AB poate fi găsit prin formula:

Programul „Calcularea distanței dintre două linii și coordonate toate comune perpendiculara.“

Programul „Calcularea distanței dintre două linii și coordonate toate comune perpendiculara.“

Eliberat valoarea curentă de coordonate coordonează toate comune perpendicular pe liniile AB și CS ca o ireductibilă rațională fracție c / r.
Eliberat valoarea distanței curentului între două linii în formă de c * sqrt (p) / r

Fraction c / r este fracție rațională ireductibilă, iar expresia p radicand nu conține ca divizorii pătrate numere naturale.

Rezultatul poate fi afișat în fișierul.

Pentru a muta cursorul la câmpul următor și calculează rezultatele, utilizați tasta Enter.