Accelerare - media, instantanee, tangențială, normal, plin
Unitatea SI de accelerare se numește 1 metru pe secundă pe secundă (metri pe secundă la pătrat)
Accelerarea caracterizează viteza de schimbare a vitezei.
De exemplu, o masina care este pornit, se mișcă rapid, deoarece viteza de circulație crește. Viteza Punctul de pornire a vehiculului este zero. Pornind de mișcare, vehiculul este accelerat la o anumită viteză. Dacă este necesar, încetini, masina nu se va opri imediat, dar de ceva timp. Adică, viteza vehiculului va tinde la zero - mașina începe să se miște într-un încetinit-up până la oprire completă. Dar fizica nu este termenul „decelerarea“. În cazul în care organismul este în mișcare, reducând viteza acestui proces este, de asemenea, numit accelerație. dar cu semnul „-“.
accelerație medie.
accelerare medie este raportul dintre rata de modificare a duratei de timp în care are loc schimbarea. Calculând o accelerație medie cu formula:
,
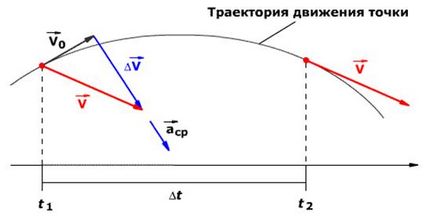
unde - este vectorul accelerație. Direcția vectorului accelerație este aceeași ca și rata de schimbare a direcției δ = - 0
unde 0 este viteza inițială. La momentul t1 momentul (vezi. Fig. De mai jos) corpul 0. La momentul t2 viteza corpului are. Pe baza regulilor de scădere a vectorilor, definim rata de schimbare a vectorului ö = - 0. Prin urmare vom calcula accelerația:
.
Unitatea SI de accelerare se numește 1 metru pe secundă pe secundă (metri pe secundă la pătrat):
.
Metru pe secundă la pătrat - această accelerare se deplasează rectiliniu punctul în care rata de 1 s crește de la acest punct de 1 m / s. Cu alte cuvinte, aceasta determină viteza de accelerare a vitezei de schimbare a corpului 1. De exemplu, dacă accelerația este de 5 m / sec 2. Viteza medie a corpului în fiecare secundă crește cu 5 m / s.
accelerare instantanee.
accelerare instantanee a corpului (punct material) într-un timp dat - este o cantitate fizică. care este egală cu limita față de care accelerația medie tinde intervalul de la 0. Cu alte cuvinte - această accelerare a dezvoltat de organism pentru o perioadă de timp foarte limitată:
.
Accelerația are aceeași direcție ca ö rata de schimbare într-o perioadă foarte mică de timp pentru care rata variază. Vectorul accelerație poate fi setat prin intermediul proiecțiilor pe axa de coordonate respective într-un cadru de referință predeterminat (proiecții AXE. Ay. AZ).
Cu viteză accelerată mișcare rectilinie a creșterilor corpului în modul, adică v2> v1. și vectorul accelerație are aceeași direcție cu cea a vectorului de viteză 2.
Dacă viteza corpului este redus modulo (v2 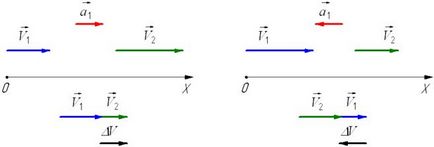
Dacă există o mișcare de-a lungul unui traseu curbat, magnitudinea și direcția de schimbare de viteză. Deci, vectorul accelerație este reprezentat sub formă de 2 componente.
accelerare tangential.
Tangențială (tangent) se face referire la componenta de accelerare a vectorului accelerație care este tangentă la traiectoria în acel punct traiectorie. accelerația tangențială descrie extinderea ratei de schimbare în modul în comiterea mișcării curbilinii.
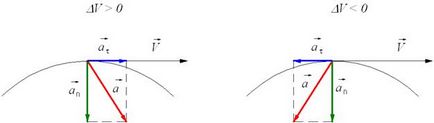
La vectorul uskoreniyaτ tangențială (vezi. Fig. De mai sus) în aceeași direcție ca și cea a vitezei liniare sau opusă acesteia. Ie vectorul accelerație tangențial stocate într-o singură axă tangenta la un cerc care este traiectoria de mișcare a corpului.
accelerație normală.
accelerație normală este acea porțiune a vectorului accelerație, care este perpendicular pe direcția mișcării la un anumit punct de pe traiectoria de mișcare a corpului. Ie vectorul accelerație normală este perpendiculară pe viteza liniară (vezi. fig. de mai sus). accelerație normală descrie extinderea ratei de schimbare de direcție și este desemnată ca n. vector accelerație normală este direcționată de-a lungul razei de curbură a traiectoriei.
accelerație maximă.
Full mișcare accelerare curbilinie este compus dintr-un tangențiale și normale vectori de accelerație de regulă plus și se calculează cu ajutorul formulei:
(Pitagoreic pentru o cutie dreptunghiulară). Cu ajutorul unor reguli de adiție vectoriale și se calculează direcția de accelerație maximă: